信号 第六章：信号与系统的复频域分析

6.1 拉氏变换的定义

双边：（必须注明收敛域）

$$\begin{cases} X(s)=\int_{-\infty}^\infty x(t)e^{-st}dt\\ x(t)=\frac1{2\pi j}\int_{σ-j\infty}^{σ+j\infty}X(s)e^{st}ds \end{cases}$$

单边：（不需加注收敛域）

$$\begin{cases} \tilde X(s)=\int_{0^-}^\infty x(t)e^{-st}dt\\ x(t)=\frac1{2\pi j}\int_{σ-j\infty}^{σ+j\infty}\tilde X(s)e^{st}ds \end{cases}$$

其中$s=\sigma+j\omega$，$\sigma$对应引入的衰减因子$e^{-\sigma t}$，使更多不满足收敛条件从而无法进行傅里叶变换的函数可以进行变换。

---

一个连续信号$x(t)$拉氏变换存在的条件是被积函数为收敛函数，即：

$$\int_{-\infty}^{\infty}|x(t)e^{-st}|dt<\infty$$

上式的存在取决于$σ$值的选择，$σ$的取值范围就是拉氏变换的收敛域。

---

$X(s)$可表示为：

$$X(s)=\frac{b_0+b_1s+...+b_ms^m}{a_0+a_1s+...+a_ns^n}=\frac{A\prod_{i=1}^m(s-z_i)}{\prod_{j=1}^n(s-p_j)}$$

式中：$A=b_m/a_n$，$z_i$是$X(s)$的零点， $p_j$是$X(s)$的极点。

---

$x(t)$的时域特性与其$X(s)$收敛域的关系：

性质①：$X(s)$的收敛域在$s$平面内由平行于$j\omega$轴的带状区域所组成；

性质②：对于有理拉氏变换来说，收敛域内不应包括任何极点；

性质③：若$x(t)$是有限连续时间信号， 且绝对可积，其收敛域为整个$s$平面；

性质④：若$x(t)$是右边信号， 且$X(s)$存在，则$X(s)$的收敛域在其最右边极点的右半边；

性质⑤：若$x(t)$是左边信号， 且$X(s)$存在，则$X(s)$的收敛域在其最左边极点的左半边。

6.2 常用信号的拉氏变换对

$$\begin{aligned} \delta(t)\Leftrightarrow 1,[全部s]&\quad\quad\quad \delta(t-T)\Leftrightarrow e^{-Ts} ,[全部s]\\ u(t)\Leftrightarrow\frac1s,[Re\{s\}>0]&\quad\quad\quad -u(-t)\Leftrightarrow\frac1s,[Re\{s\}<0]\\ e^{-at}u(t)\Leftrightarrow\frac1{s+a},[Re\{s\}>-a]&\quad\quad\quad -e^{-at}u(-t)\Leftrightarrow\frac1{s+a},[Re\{s\}<-a]\\ \frac{t^{n-1}}{(n-1)!}u(t)\Leftrightarrow \frac{1}{s^{n}},[Re\{s\}>0]&\quad\quad\quad \frac{t^{n-1}}{(n-1)!}e^{-at}u(t)\Leftrightarrow \frac{1}{(s+a)^{n}},[Re\{s\}>-a]\\ \cos\omega_0tu(t)\Leftrightarrow\frac{s}{s^2+\omega_0^2},[Re\{s\}>0]&\quad\quad\quad \sin\omega_0tu(t)\Leftrightarrow\frac{\omega_0}{s^2+\omega_0^2},[Re\{s\}>0]\\ e^{-at}\cos\omega_0tu(t)\Leftrightarrow\frac{s+a}{(s+a)^2+\omega_0^2},[Re\{s\}>-a]&\quad\quad\quad e^{-at}\sin\omega_0tu(t)\Leftrightarrow\frac{\omega_0}{(s+a)^2+\omega_0^2},[Re\{s\}>-a]\\ \end{aligned}$$ $$e^{-b|t|}\Leftrightarrow \frac{-2b}{s^2-b^2}\quad,[-b<Re\{s\}<b]\\ \begin{cases} e^{\alpha_2t}&,{t<0}\\ e^{\alpha_1t}&,{t>0} \end{cases}=e^{\alpha_2t}u(-t)+e^{\alpha_1}u(t)\Leftrightarrow \frac{\alpha_1-\alpha_2}{(s-\alpha_1)(s-\alpha_2)}\quad,[\alpha_1<Re\{s\}<\alpha_2]$$

---

周期信号的拉氏变换：

这里所指的周期信号是指仅在$t\ge 0$时存在的单边周期信号$x(t)$，而$t<0$时$x(t)=0$。

令周期信号的第一个周期的时间函数为$x_1(t)$，则有：

$$X(s)=\frac{X_1(s)}{1-e^{-sT}}$$

6.3 双边、单边拉氏变换的性质

①. 线性

$$ax_1(t)+bx_2(t)\Leftrightarrow aX_1(s)+bX_2(s)\quad ,ROC至少包含R_1∩R_2$$

若$R_1∩R_2$是空集，表示$ax_1(t)+bx_2(t)$的拉氏变换不存在。当$aX_1(s)$和$bX_2(s)$在相加过程中发生零极点相抵消，则收敛域还可能扩大。

②. 时移

$$x(t-t_0)\Leftrightarrow e^{-st_0}X(s)\quad ,收敛域不变，同X(s)$$

③. S域平移

$$e^{at}x(t)\Leftrightarrow X(s-a)\quad ,ROC=R+Re\{a\}$$

④. 尺度变换

$$x(at)\Leftrightarrow \frac1{|a|}X(\frac sa)\quad ,ROC=a\cdot R$$

⑤. 时域微分

$$\begin{aligned} 双边：&\frac{dx(t)}{dt}\Leftrightarrow sX(s)\quad ,ROC至少包含R\\ 单边：&\frac{dx(t)}{dt}\Leftrightarrow s\tilde X(s)-x(0^-)\\ &\frac{d^2x(t)}{dt^2}\Leftrightarrow s^2\tilde X(s)-sx(0)-x'(0) \end{aligned}$$

⑥. s域微分

$$-tx(t)\Leftrightarrow \frac{dX(s)}{ds}\quad,ROC不变$$

⑦. 时域积分

$$\begin{aligned} 双边：&\int_{-\infty}^tx(\tau)d\tau\Leftrightarrow \frac1s{\tilde X(s)}\\ 单边：&\int_{-\infty}^tx(\tau)d\tau \Leftrightarrow \frac{\tilde X(s)}{s}+\frac{x^{-1}(0^-)}{s}\\ &x^{-1}(0^-)=\int_{-\infty}^{0^-}x(\tau)d\tau \end{aligned}$$

⑧. 卷积

$$\begin{aligned} 双边：&x(t)\star h(t)\to X(s)H(s)\quad,收敛域至少包含R_1∩R_2\\ 单边：&若x_1(t)、x_2(t)都是单边信号，则x_1(t)\star x_2(t)\Leftrightarrow \tilde X_1(s)\tilde X_2(s) \end{aligned}$$

⑨. 初值定理和终值定理

若$t<0$时，$x(t)=0$，则：

$$\begin{aligned} 初值定理：&x(0^+)=\lim_{s\to\infty}sX(s)\\ 终值定理：&\lim_{t\to\infty}x(t)=\lim_{s\to 0}sX(s) \end{aligned}$$

6.4 拉氏反变换

仅讨论可以用有理函数表示的拉氏函数的反变换

$$X(s)=\frac{N(s)}{D(s)}=\frac{b_0+b_1s+...+b_ms^m}{a_0+a_1s+...+a_ns^n}$$

利用部分分式法进行展开求反变换：

①. $X(s)$分母多项式有$n$个互异实根：

$$\begin{aligned} X(s)&=\frac{N(s)}{a_n(s-p_1)(s-p_2)...(s-p_n)}\\ &=\frac{k_1}{s-p_1}+\frac{k_2}{s-p_2}+...+\frac{k_n}{s-p_n} \end{aligned}$$

式中各系数：

$$k_i=X(s)(s-p_i)|_{s=p_i}$$

②. $X(s)$分母多项式中含有重根：

$$\begin{aligned} X(s)&=\frac{N(s)}{(s-p_1)^kD_1(s)}\\ &=\frac{k_{11}}{(s-p_1)^k}+\frac{k_{12}}{(s-p_1)^{k-1}}+...+\frac{k_{1k}}{(s-p_1)}+\frac{B(s)}{D_1(s)} \end{aligned}$$

式中各系数：

$$k_{11}=X(s)(s-p_1)^k|_{s=p_1}\\ k_{12}=\frac{d}{ds}[X(s)(s-p_1)^k]|_{s=p_1}\\ k_{13}=\frac12\frac{d^2}{ds^2}[X(s)(s-p_1)^k]|_{s=p_1}\\ ...\\ k_{1i}=\frac1{(i-1)!}\frac{d^{(i-1)}}{ds^{(i-1)}}[X(s)(s-p_1)^k]|_{s=p_1}\\$$

6.5 系统的复频域分析

$e^{st}$是CT LTI系统的特征函数

---

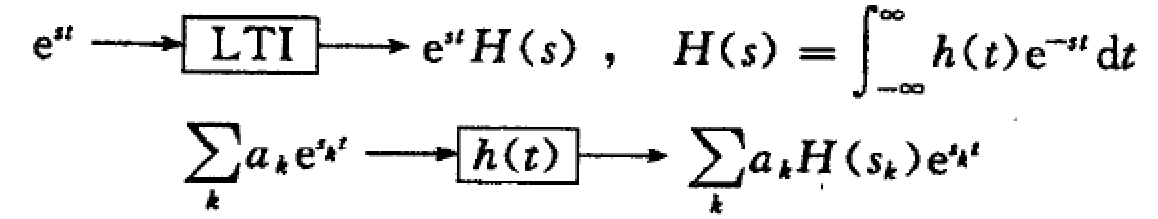
系统函数$H(s)$及微分方程$s$域求解：

$$\sum_{k=0}^Na_k\frac{d^{(k)}y(t)}{dt^k}=\sum_{k=0}^Mb_k\frac{d^{(k)}x(t)}{dt^k}$$

对微分方程进行双边拉氏变换后可得系统函数为：

$$H(s)=\frac{Y_{zs}(s)}{X(s)}=\frac{\sum_{k=0}^Mb_ks^k}{\sum_{k=0}^Na_ks^k}$$

当$H(s)$的收敛域包括虚轴时，可得$H(j\omega)$

从$H(s)$的零、极点可在$s$平面上画出系统的频率响应$H(j\omega)$

---

根据$H(s)$的零、极点分布可判定系统的因果性和稳定性：

①. 因果性：对于一个因果LTI系统，当$t<0$时，$h(t)=0$，即$h(t)$是一个右边信号，故$H(s)$的收敛域应在最右边极点的右半平面。

②. 稳定性：稳定的系统$H(s)$的收敛域必包含$j\omega$轴

③. 因果稳定性：

若因果稳定系统的系统函数其全部极点分布在$s$左半平面，收敛域包括$j\omega$轴，系统稳定；若$H(s)$的极点中有一个位于$s$平面右半平面，则系统不稳定。

若极点中除了$s$平面的左半面上有极点外，只要在$j\omega$轴上有一对共轭的单阶极点，或在坐标原点上有一个单阶极点，则系统是临界稳定的（稳定与不稳定的边界，实际不稳定）。

---

全响应的求解：

法①：直接从微分方程的起始状态求出零输入响应，再加上$Y_{zs}(s)=X(s)H(s)\to y_{zs}(t)=L^{-1}\{X(s)H(s)\}$，即可得到全响应。

法②：利用单边拉氏变换可一次求出系统的全响应$y(t)$，零输入$y_{zi}(t)$和零状态$y_{zs}(t)$。

知识点补充

①. 若一个系统的$H(x)$的极点多于零点，则其阶跃响应在$t=0$上是连续的；

②. $x(t)=1$可看作$x(t)=e^{j0t}$，则$y(t)=e^{j0t}\cdot H(0)$

③. $x(t)$是偶函数，则$X(s)$必定是偶函数（从定义式可推导）。

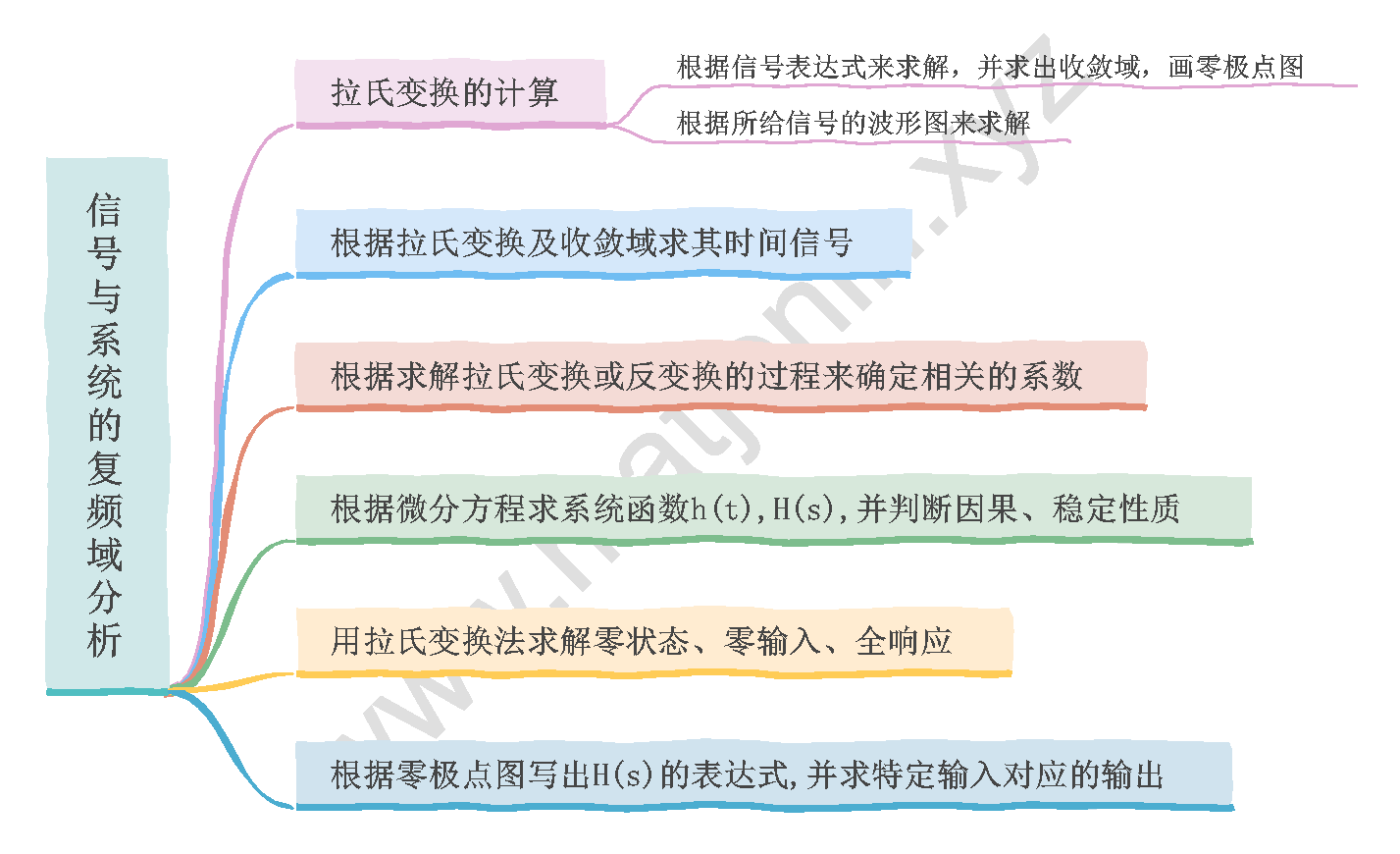
题型总结