微波技术 第二章 传输线理论
2.1 引言
传输线:传输微波的专用电缆或者其他结构。
微波传输线的形态:双导线(平行线)、同轴电缆、带状线、微带线。
双导线与低频传输线有着本质的不同:功率通过双导线之间的空间传输。
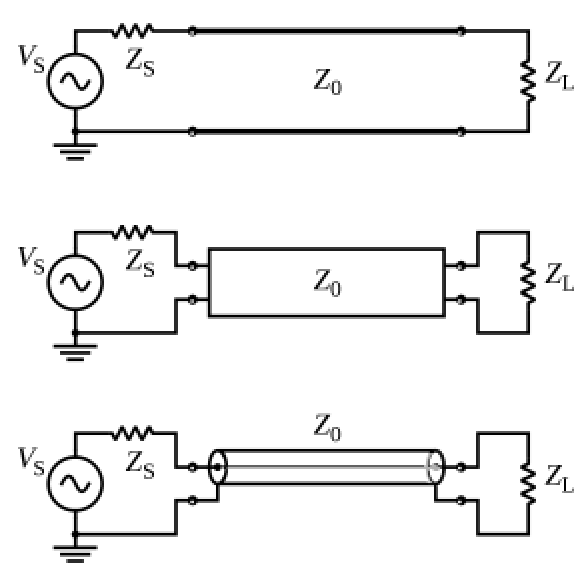
了解:为什么用传输线?
集肤效应。当频率升高时,导体的电流、电荷和电池都集中在导体表面。
产生集肤效应的原因:变换的电磁场在导体内部产生涡旋电场,抵消原有电流。
集中参数:当元件尺寸远远小于工作波长时,可用特定参数表示该元件的特性,参数导线上的电压和电流不随时空变换。集中参数元件:电阻、电容、电感。集中参数电路分析方法:基尔霍夫电路定律。
分布参数:模型参数与工作特性既是时间的函数,还与元件尺寸、空间坐标有关。要用场的分析方法,根据麦克斯韦方程表征场的作用和传递。
2.2 传输线方程
1. 通过基尔霍夫定律推导出电压波和电流波的波动方程
2. 求解波动方程可得电压波和电流波表达式,并可以得出特征阻抗
3. 将边界条件代入电压波和电流波表达式,可以得到矩阵形式的表达式
2.2.1 传输线方程
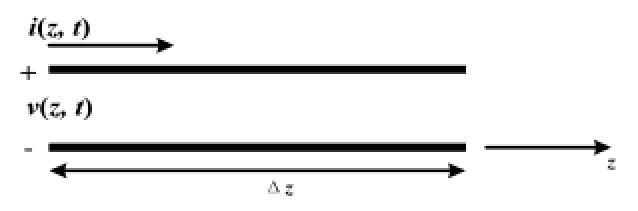
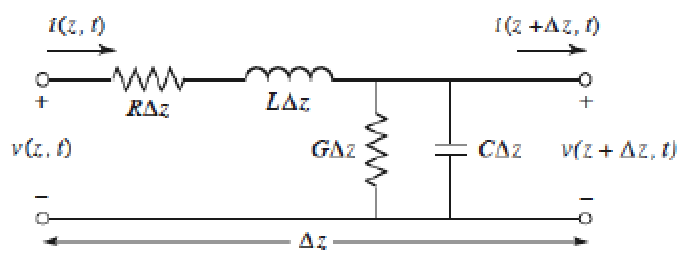
$R(Ω/m)、L(H/m)、C(F/m)、G(S/m)$:两导体单位长度的串联电阻、串联电感、并联电容、并联电导。
基尔霍夫电压定律:
基尔霍夫电流定律:
等式两边除以$△z$,并取$△z→0$,可得
简谐稳态时,电压和电流具有余弦型向量形式,即
联立$①②$,可得关于$V(z)$和$I(z)$的波动方程:
复传播常数:$\gamma=\alpha+j\beta=\sqrt{(R+j\omega L)(G+j\omega C)}$
$\alpha$:衰减常数,$Np/m$;$\beta$:相位常数,$rad/m$
对于理想传输线(无损),$\alpha=0;R,G=0$,$\gamma=j\beta=j\omega\sqrt{LC}$。(2020年考到)
求解$V(z)$和$I(z)$的波动方程可得:
其中,$V^+_0、V^-_0、I^+_0、I^-_0$由边界条件决定。
通常用$e^{j\omega t\pm \gamma z}$表示波,$e^{j\omega t-\gamma z}$和$e^{j\omega t+\gamma z}$分别代表沿$+z$方向和沿$-z$方向传播的波,即入射波和反射波。
如果不考虑损耗$\alpha=0$,入射波和反射波可以分别表示为$e^{j(\omega t-\beta z)}$和$e^{j(\omega t+\beta z)}$。
假设$z$轴正方向从源指向负载,$e^{j(\omega t-\beta z)}$的固定相位点满足$\omega t-\beta z=C$(常数),则相速度为:
2.2.2 特征阻抗
将$V(z)$表达式代入到$\frac{dV(z)}{dz}=-(R+j\omega L)I(z)$中,则
定义传输线的特征阻抗:
无耗传输线:$\alpha=0,R=G=0$,传播常数$\gamma=j\beta=j\omega \sqrt{LC}$,此时$Z_0=\frac{L}{C}$。$V(z)$和$I(z)$可表示为:
2.2.3 边界条件
若已知负载处$(z=0)$,$V(0)=V_L,I(0)=I_L$,则有如下关系:
将$V^+_0$和$V_-$代入电压波和电流波的表达式,整理可得:
若传输线的长度为$l$,负载在$z=0$处,传输线输入端$z=-l$的电压波和电流波为:
写成矩阵形式:
2.3 传输线的状态及参量
2.3.1 输入阻抗
输入阻抗$Z_{in}$:传输线上任意一点电压与电流之比。
其中,$Z_L=\frac{V_L}{I_L}$
其中$Y_L=\frac1{Z_L},Y_0=\frac1{Z_0}$
输入阻抗$Z_{in}$具有周期性,$\beta=2\pi/\lambda$,无耗传输线上任意相距$\lambda/2$处的阻抗相同。
传输线上$z=-l-\frac{\lambda}{4}$处的输入阻抗为:
说明$\frac{\lambda}4$传输线具有阻抗变换的作用,称为四分之一波长变换器。
定义归一化阻抗为$\overline Z=\frac{Z}{Z_0}$,那么
表明传输线上相隔$\frac{\lambda}{4}$的两点,其归一化输入阻抗互为倒数。
2.3.2 反射系数
传输线某处的反射系数,定义为该处的反射电压波(或电流波)和入射电压波(或电流波)之比,用$\Gamma(z)$来表示,即
反射系数$\Gamma(z)$反映入射波与反射波振幅和相位的差异。
2.1.3节提到,若已知负载处$(z=0)$,$V(0)=V_L,I(0)=I_L$,则有如下关系:
在负载处($z=0$),反射系数为
将$(1)$代入到$\Gamma(z)$表达式中,得
由此可见,无耗传输线上各处反射系数模值相同,幅角随该处与负载距离的变化而变化。
将$(1)$带入,电压波和电流波可表达为,
传输线上任意一点的输入阻抗:
负载处$Z_{in}(0)=Z_L,\Gamma(0)=\Gamma_L$,有
当$Z_L=Z_0$时,$\Gamma_L=0$,即负载终端无反射,此时传输线上的反射系数$\Gamma(z)=\Gamma_Le^{j2\beta z}$处处为零,称为阻抗匹配。
2.3.3 电压驻波比
电压波幅度最大值位于入射波和反射波相位相同处,而幅度最小值位于入射波和反射波的相位相反处,即
其中$|\Gamma(z)|=|V_0^-|/|V_0^+|$,取值范围$0\le |\Gamma(z)|\le 1$。
电压驻波比ρ定义为传输线上波幅点电压振幅与波节点电压振幅之比,即
取值范围$0\le|\Gamma(z)|\le 1$。
- 当阻抗匹配$(Z_L=Z_0)$时,$|\Gamma(z)|=|\Gamma_L|=0,ρ=1$;
- 当波被负载全部反射时,$|\Gamma(z)|=|\Gamma_L|=1,ρ=\infty$
定义$l_{min,0}$:从负载$(z=0)$向信号源方向移动到最近一个波节点的距离。推导可得:
2.4 传输线的工作状态
传输线的工作状态是指终端接不同负载时,沿线电压和电流的分布状态。
2.4.1 行波状态
阻抗匹配,无反射波,称为行波状态。
行波状态时电压波和电流波的表达式:
输入阻抗:
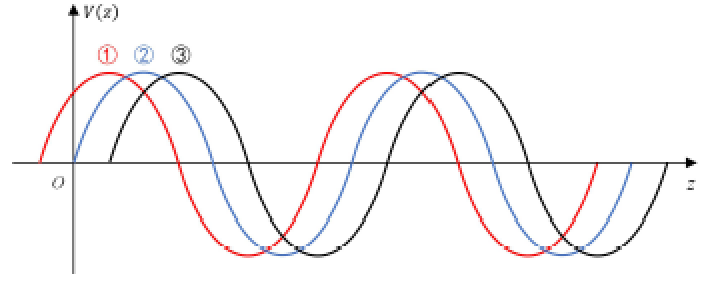
考虑瞬时形式:
其中$V_0^+=|V_0^+|e^{j\phi_0}$
红$(\omega t=0)$,蓝$(\omega t=\frac{\pi}{4})$,黑$(\omega t=\frac{\pi}{2})$
2.4.2 纯驻波状态
纯驻波状态:$|\Gamma|=1$的全反射情况。
定理:传输线全反射的条件是负载端接纯电抗,即$Z_L=jX_L$(推导略)。
纯驻波状态——短路状态
短路状态:$Z_L=0$,此时$\Gamma_L=-1$,$V_0^-=-V_0^+$,$ρ=\infty $
电压波和电流波表达式:
输入阻抗为:
短路传输线上会周期性地出现电压和电流的波腹点和波节点。
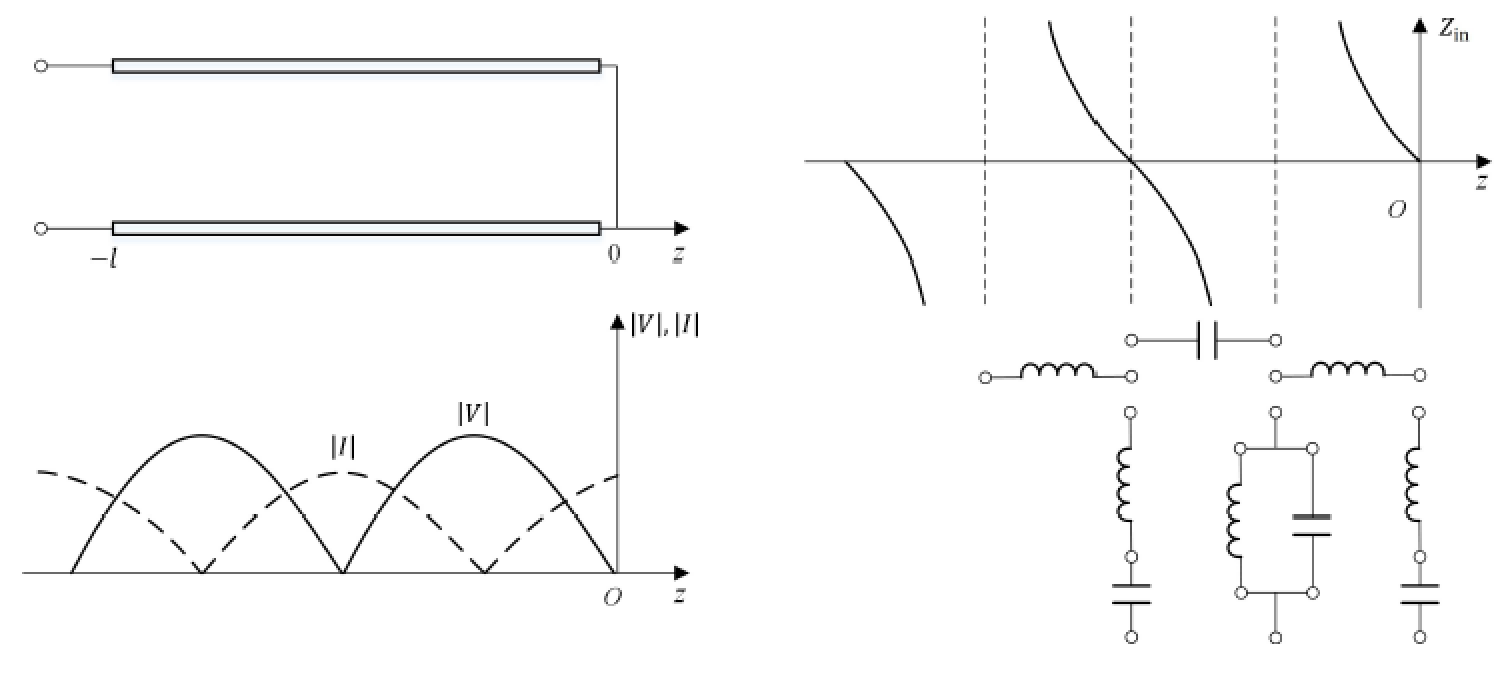
纯驻波状态——开路状态
开路状态:$Z_L=\infty$,此时$\Gamma_L=1,V_0^-=V_0^+,ρ=\infty$
电压波和电流波的表达式:
输入阻抗:
开路传输线上也会周期性地出现电压和电流的波腹点和波节点。
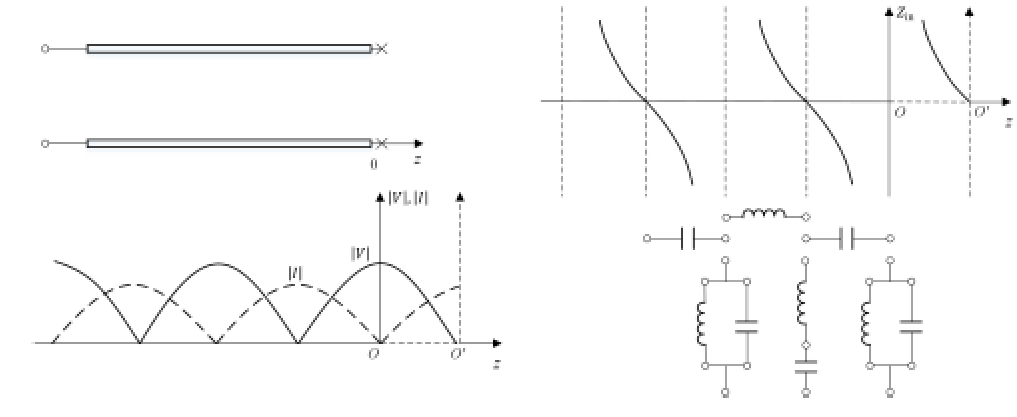
终端开路传输线是延伸(或缩短)$\frac{\lambda}{4}$的终端短路传输线。
纯驻波状态——任意电抗负载
传输线端接任意电抗负载$Z_L=jX_L$
推导可得:
电压波的表达式(推导):
电流波的表达式(推导):
输入阻抗为:
2.4.3 行驻波状态
一般的部分反射情况。
电压波和电流波表达式(推导):
传输线上电压波和电流波的模值(推导):
其中$l\ge 0$
①. 当$\theta_L-2\beta l=2n\pi$时,$\cos(\theta_L-2\beta l)=1$,有
此时的电压波、电流波和输入阻抗表示为:
②. 当$\theta_L-2\beta l=(2n+1)\pi$时,$\cos(\theta_L-2\beta l)=-1$,有
此时的电压波、电流波和输入阻抗表示为:
2.4.4 平均功率
传给负载的功率(推导):
即传输功率等于入射波功率减去反射波功率。
2.6 原图及其应用
2.6.1 反射系数复平面
反射系数范围$0\le |\Gamma|\le 1$,反射系数复平面为:

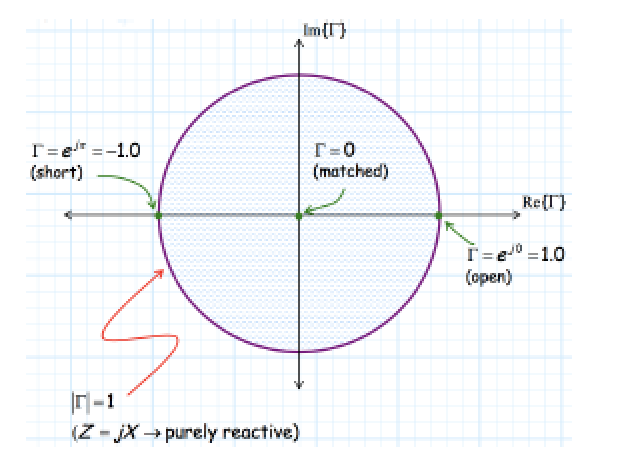

给在负载前添加一段传输线,等效于给负载端的反射系数幅角顺时针旋转$2\beta l$角度,而反射系数的模值$|\Gamma|$不变。

已知输入端的反射系数,求负载端的反射系数时,需要逆时针旋转输入端的反射系数。

2.6.2 推导史密斯原图
上式表示在反射系数复平面上的一簇圆,这些圆以$(\frac{r}{1+r},0)$为圆心,以$\frac1{1+r}$为半径,与归一化的电抗$x$无关,被称为等电阻圆。

上式表示在反射系数复平面上的一簇圆,这些圆以$(1,\frac1x)$为圆心,以$\frac1x$为半径,与归一化的电阻$r$无关,被称为等电抗圆。

将等电阻圆和等电抗圆同时放在反射系数复平面上,就是史密斯原图。横轴为纯电阻线,$r=0$即$|\Gamma|=1$的圆为纯电抗线。


以原点为圆心,$|\Gamma_L|\le 1$为半径做出的圆,代表着传输线上任意一点$(z=-l)$的反射系数。在这个圆上,反射系数的模值相同,但是相位不同。
2.6.3 史密斯原图与电压驻波比
电压驻波比:
输入阻抗和归一化输入阻抗:
找到电压驻波比$ρ$和归一化输入阻抗$z_{in}(-l)$能够相互转化的条件:
①. 当$\Gamma(-l)=|\Gamma_L|$时,
等效于反射系数复平面横轴的正半部分$Re\{\Gamma\}\ge 0$
②. 当$\Gamma(-l)=-|\Gamma_L|$时,
等效于反射系数复平面横轴的负半部分$Re\{\Gamma\}\le0$
2.6.4 如何使用史密斯原图
用直尺或圆规记录下某一阻抗的反射系数的模值,该模值是史密斯原图中心点和某一阻抗值的距离。而后在特定标尺上以CENTER为起点,找到该距离对应的数值。
以状态参量$\Gamma$的模$|\Gamma|$为基底,消去特征阻抗$Z_0$,把相位常数$\beta$归于$\Gamma$的相位,映射归一化输入阻抗$z_{in}(-l)$和电压驻波比$ρ$。
2.6.5 从阻抗圆图到导纳圆图
阻抗圆图和导纳圆图有相同的形式,但是有不同的物理意义。
阻抗圆图的等电阻圆和等电抗圆,分别对应着导纳圆图的等电导圆和等电纳圆。
纯电抗线($r=0,|\Gamma|=1$)的上半圆为感性,下半圆为容性;纯电纳线($g=0,|\Gamma|=1$)相反。
导纳圆图的开路点和短路点与阻抗圆图的相反。
对于导纳圆图,从负载到源和从源到负载依旧分别是顺时针和逆时针旋转。
2.6.6 导纳圆图实现阻抗匹配——单枝节匹配
$y_{in}(-l)=1$,待求解参量为主传输先长度$l$和枝节长度$d$

Stub处可以代表开路或短路两种情况。
要求网络总的归一化电导为1:
根据并联网络的关系,有
由于枝节从导纳圆图短路点(1,0)或开路点(-1,0)出发,在传输线上其导纳只能是纯电纳(也可理解为原负载被归一化后需要将电纳部分抵消,才能将总输入导纳归一化),因此
四种方法:




2.6.7 导纳圆图实现阻抗匹配——双枝节匹配

同样要求网络总的归一化电导为1:$y_2(-l_2-l_1)=1+j0=1$
根据并联网络的关系,有:$y_2(-l_2-l_1)=y’_2(-l_2-l_1)+y’’_2(-d_2)$
由于枝节从导纳圆图短路点(1,0)或开路点(-1,0)出发,在传输线上其导纳只能是纯电纳(也可理解为原负载被归一化后需要将电纳部分抵消,才能将总输入导纳归一化),因此有
2.6.8 导纳圆图实现阻抗匹配——双枝节匹配
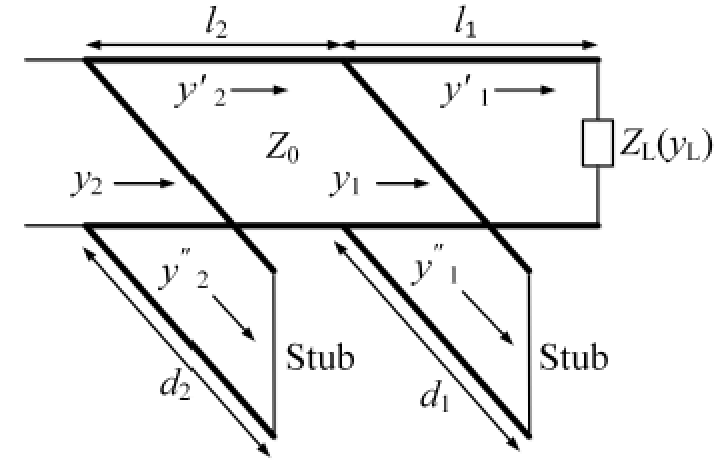
主传输线长度固定$(l_1,l_2已知)$,直接长度可调$(确定d_1,d_2)$。
最终的结果要求网络的归一化电导为1:$y_2(-l_2-l_1)=1.0+j0=1.0$,即史密斯原图的原点。
根据并联网络的关系,有
由于枝节从导纳圆图短路点(1,0)或开路点(-1,0)出发,在传输线上其导纳只能是纯电纳(也可理解为原负载被归一化后需要将电纳部分抵消,才能将总输入导纳归一化),因此
导纳$y’_2(-l_2-l_1)=1+jb_2$处在$g=1$等电导圆,通过传输线$l_2$由第二个枝节到达第一个枝节,等效于在圆图上从$1+jb_2$出发,沿等反射系数模值圆逆时针旋转$l_2$所对应的角度。
相应的,$g=1$等电导圆逆时针旋转$l_2$所对应的角度,变为$z=-l_1$处的辅助圆。
如果$l_2=\frac{\lambda}{8}$,对应旋转角度为$2\beta l_2=2\frac{2\pi}{\lambda}\frac{\lambda}{8}=\frac{\pi}{2}$
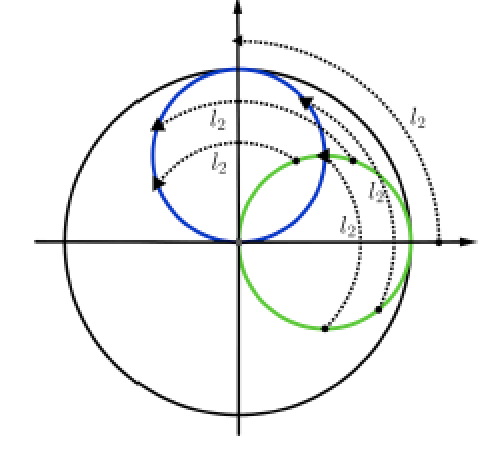
观察点从$z=-l_2-l_1$移动到$z=-l_1$意味着$g=1$的等电导圆旋转至辅助圆,这一过程中反射系数模值$|\Gamma|$不变,但是$z=-l_1$处电导$g_l$不再是1。此时,第一段传输线所对应的输入导纳为:
在史密斯圆图上,$y’_1(-l_1)$逆时针旋转$l_1$所对应的角度$2\beta l_1$便可到达负载所对应的导纳$y_L$
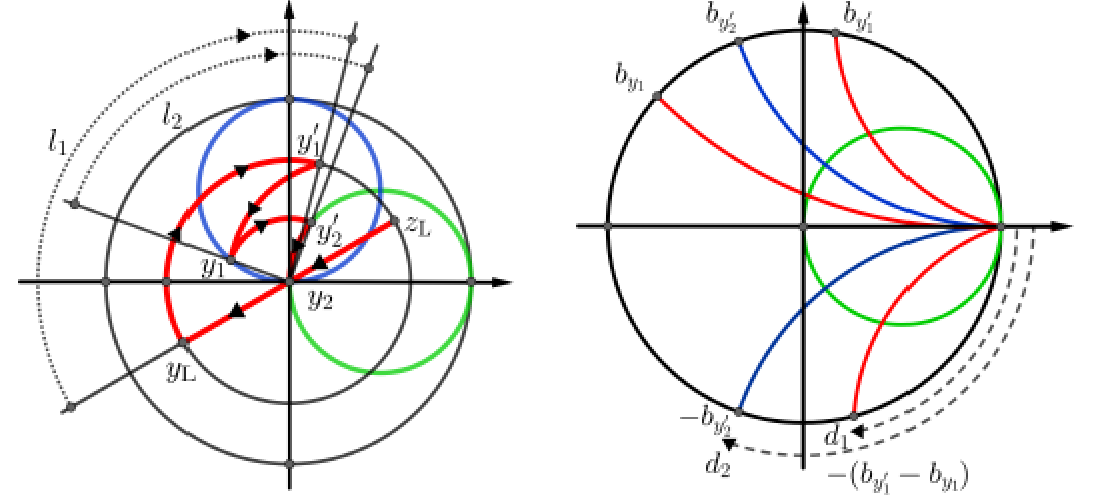
做题时的步骤:
①. 先将负载阻抗转变为导纳,然后确定导纳在史密斯图的位置;
②. 从$y_l$点的位置按等$|\Gamma|$圆顺时针旋转$l_1$到达$y’_1$($y’_1$的实部为$g_l$),此时可以;
③. 按等电导圆$g_l$与辅助圆交于$y_1$,此时可以计算出$d_1$,方法为$y_1$和$y’_1$虚部相减;
④. 从$y_1$点按等$|\Gamma|$顺时针旋转$l_2$到达$y’_2$,因为$y_2=1$,所以此时可以计算出$d_2$,即$y_2’$的虚部的相反数。
2.7 阻抗匹配
类型:
- 负载阻抗匹配:$Z_L=Z_0$,负载阻抗等于传输线的特征阻抗,此时传输线上只有入射波,没有反射波;
- 源阻抗匹配:$Z_g=Z_0$,电源内阻等于传输线的特征阻抗,匹配源给传输线的入射功率不随负载而变化。负载有反射时,反射波被电源吸收;
- 共轭阻抗匹配:$Z_{in}=Z^\star_g$,负载得到最大功率的匹配方式。
2.7.1 源和负载匹配
之前研究传输线时都是假定源是匹配的,故在源端无反射发生。
令$Z_{in}=R_{in}+jX_{in}$和$Z_g=R_g+jX_g$,则一般情况下无耗传输线上传给负载的平均功率是:
负载阻抗匹配时,$Z_{in}=R_{in}+jX_{in}=Z_0=R_{in},X_{in}=0$
2.7.2 共轭匹配
当$R_{in}=R_g,X_{in}=-X_g$时,共轭阻抗匹配条件为$Z_{in}=Z^\star_g$: