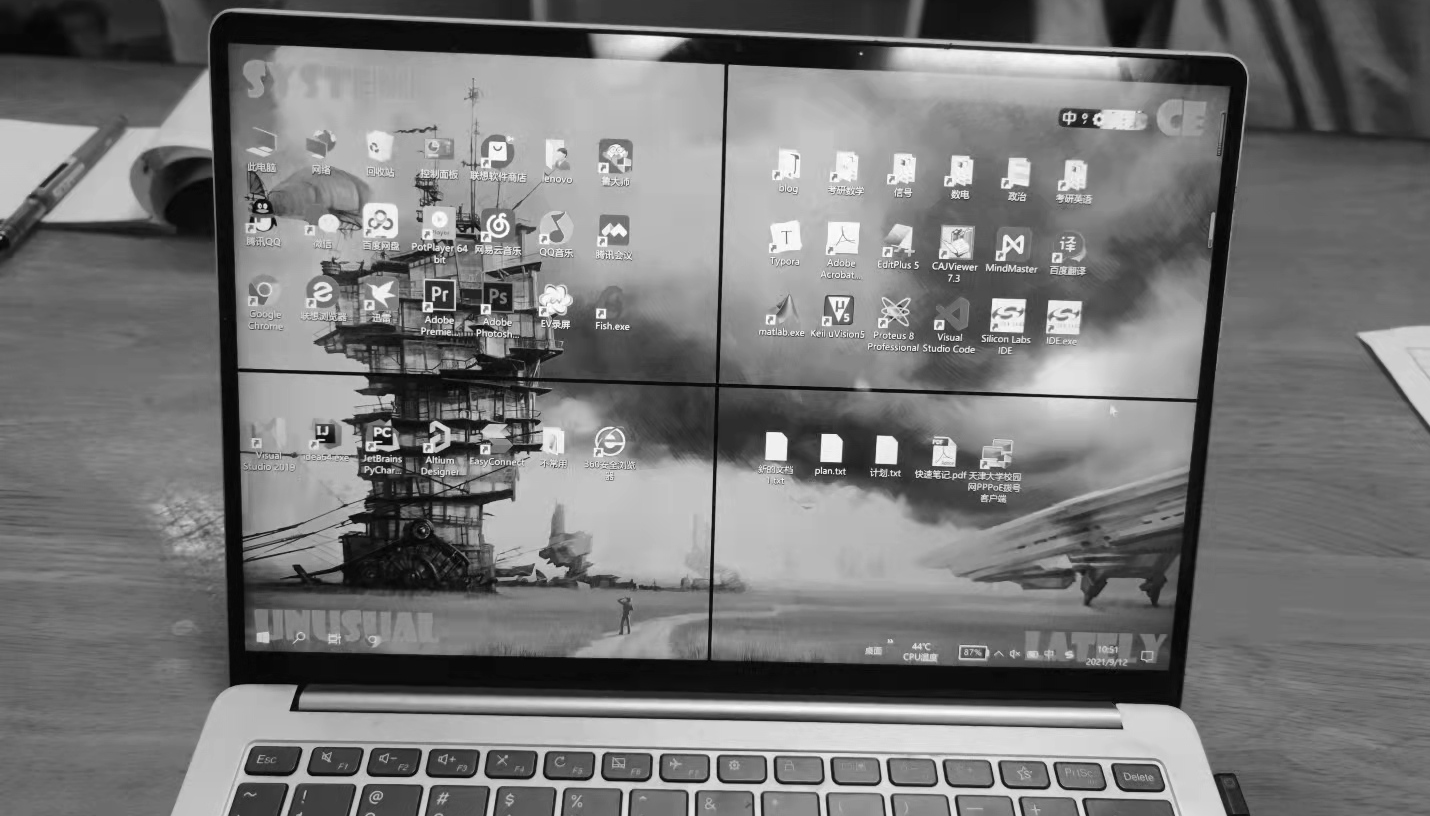
数一 李永乐660典题错题
基础过关一阶-高等数学
选择题
数列极限

解:B;①. 单调性:因为$a>1$,所以$x_2=a^{x_1}>x_1=a$,设$x_n>x_{n-1}$,故$x_{n+1}=a^{x_n}>x_n=a^{x_{n-1}}$,故$\{x_n\}$单增。
②. 有极限:$a\le e^{\frac1e}$,$x_1=a\le e$,设$x_n<e$,则$x_{n+1}=a^{x_n}\le e$,故$\{x_n\}$有上界,即有极限。
注意此题单调性和是否存在极限的证明都是用的数学归纳法,其思路为:
(1)验证$n=1$时命题$f_n$正确$\Rightarrow$假设$n=k$时命题$f_n$正确$\Rightarrow$证明$n=k+1$时,命题$f_n$正确
(2)验证$n=1$和$n=2$时命题$f_n$都正确$\Rightarrow$假设$n<k$时命题$f_n$正确$\Rightarrow$证明$n=k$时,命题$f_n$正确
函数极限

解:B;②③④都可通过极限四则运算判定。对于①,举反例$f(x)=0$,则$\lim_{x\to a}(f(x)\cdot g(x))=0$。
引申出一个结论:若$\lim_{x\to a}f(x)=A,\lim_{x\to a}g(x)$不$\exists$,则:
- 当$A\ne 0$,有$\lim_{x\to a }(f(x)g(x))$不$\exists$
- 当$A=0$,不确定$\exists$不$\exists$

解:D;
对于$A$:$\lim_{x\to x_0}f(x)= \lim_{x\to x_0}g(x)$不能判断$x_0$附近$f(x),g(x)$的大小关系;
对于$B$,相当于函数极限的保号性,$A_0>B_0$应改为$A_0\ge B_0$,比如$f(x)=\frac1{x-1},g(x)=\frac{1}{(x-1)^2},x_0=1$;
对于$C$,没有假设极限存在(emmm…);
$D$相当于函数极限的保号性的正确表述。

解:A;$\lim_{n\to \infty}\sin^2[\pi(\sqrt{n^2+n}-n)]=\lim_{n\to \infty}\sin^2[\frac{n\pi}{(\sqrt{n^2+n}+n)}]=1$
无穷小

解:C;重点看③,当$n<m$时是满足的,但当$n=m$时不一定,反例:$f(x)=\sin x,g(x)=-x$
无穷大量和无界变量

解:C;此题时关于无穷大量和无界变量的区分,在基础时中已知:无穷大量一定是无界变量,反之不一定,但是可确定一子数列,无界变量沿着这一子数列时时无穷大量,即$\lim_{n\to \infty}f(x_n)=\infty$。
若$f(x)$在$[a,+\infty)$无界$\Rightarrow$对$\forall$自然数$n$,$f(x)$在$[n,+\infty)$无界$\Rightarrow \exists x_n∈[n,+\infty),|f(x_n)|>n \Rightarrow \lim_{n\to \infty}x_n=+\infty, \lim_{n\to \infty}f(x_n)=\infty$
函数和导函数连续和有界的关系

解: C;$A,B$反例:$f(x)=\frac1{x-a},f’(x)=-\frac1{(x-a)^2}$;$D$反例:$f(x)=\sqrt{x-a},f’(x)=\frac1{2\sqrt{x-a}}$
$C$可用拉格朗日中值定理证明:取定$x_0∈(a,b)$,则$\forall x∈(a,b),\exists ξ$在$x$和$x_0$之间使得:
于是$|f(x)|\le |f(x_0)|+|f’(ξ)||x-x_0|\le |f(x_0)|+M|b-a|\quad (x∈(a,b))$

解: D;非充分:$f(x)=x,f’(x)=1$;非必要:$f(x)=\sin x^2,f’(x)=2x\cos x^2$
167题说明:在有界区间上,$f’(x)$的有界性保证了$f(x)$的有界性;开区间上$f’(x)$和$f(x)$的连续性与$f(x)$的有界性无确定关系。
168题说明:在无穷区间上,$f(x)$的有界性和$f’(x)$的有界性无确定关系。
拐点

解:C;在求极值点或拐点时,除了注意一阶导或二阶导为0的点,还要注意它们不存在时的点,然后考虑两边一阶导或二阶导的正负情况。比如此题中的$x=0$处的点。
原函数的存在性

解: C;$F(x)$可导→$F(x)$连续→由原函数存在定理,$F(x)$存在原函数。
函数的可积性
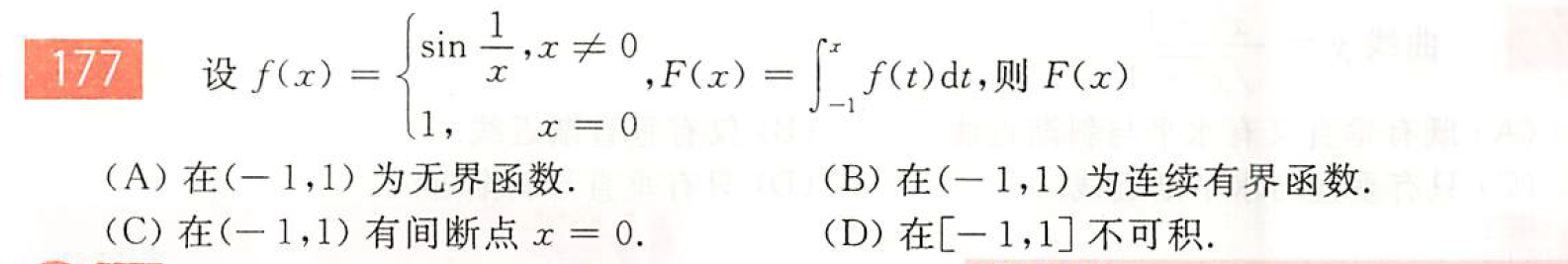
解:B; $f(x)$在$[-1,1]$上有界,只有一个间断点$x=0\Rightarrow f(x)$在$[-1,1]$可积$\Rightarrow F(x)$在$[-1,1]$上连续,因而有界。
定积分的性质

解:C;①. 正确;有条件$\Rightarrow \int_a^xf(t)dt=0(\forall x∈[a,b])$ ,则$(\int_a^xf(t)dt)’=f(x)=0$
②. 正确;有条件$\Rightarrow 0\le \int_a^xf(t)dt\le \int_a^bf(t)dt=0$,则$\int_a^xf(t)dt=0$
③. 错误
定积分和反常积分的区分
 解:B;注意定积分和反常积分的区分。$\lim_{x\to 0^+}x^n\ln^m x=0,\lim_{x\to 1}x^n\ln^m x=0$,故是定积分而不是反常积分。
解:B;注意定积分和反常积分的区分。$\lim_{x\to 0^+}x^n\ln^m x=0,\lim_{x\to 1}x^n\ln^m x=0$,故是定积分而不是反常积分。
原函数及其存在性

解: B;$f(x)$在$x=0$处不连续,故由原函数存在定理知$f(x)$在整个定义域$(-\infty,+\infty)$上不存在原函数,$F(x)$应从$x\ge 0,x\lt 0$分别考虑。

解:D;$f(x)$在$x=0$上有第一类间断点,由原函数存在定理知,$f(x)$不存在原函数;$\lim_{x\to0}g(x)=0=g(0),g(x)$在$(-1,1)$上连续,故$g(x)$存在原函数。
反常积分的收敛性
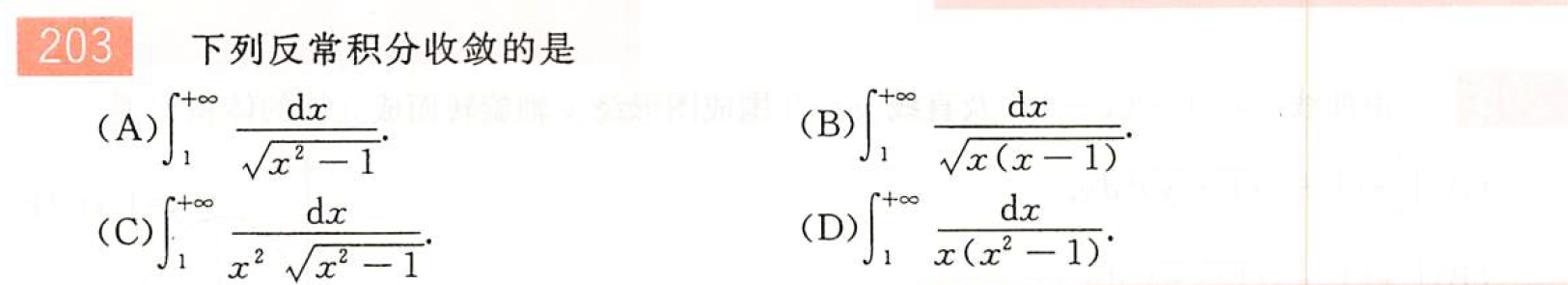
解:$A,B,C,D$在$x=1$处均无定义,不能使用比较判别法(细节,需要警惕),需要直接利用定积分计算方法来计算。
反常积分收敛的比较判别法:
前提:$f(x),g(x)$在$[a,+\infty]$连续非负(注意区间左侧为闭)
①. 比较原理:大收敛→小收敛,小发散→大发散;
②. 比较原理的极限形式。

解:A;明显③√④×。①. 反例:$\int_{-\infty}^{+\infty}\sin xdx$发散;②. 反例:$\lim_{R\to \infty}\int_{-R}^R \sin xdx=0$
多元函数的极限
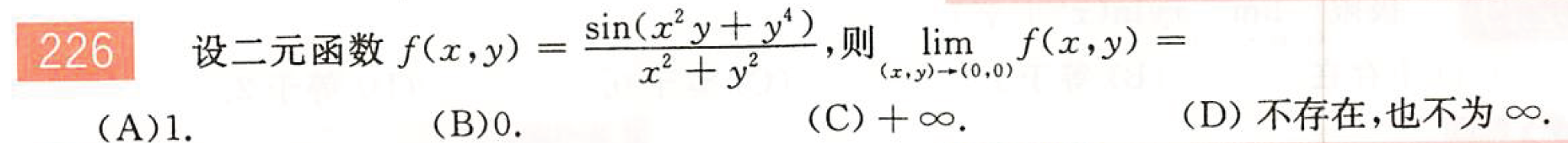
解: B;
多元函数极限通常通过不等式变换利用夹逼定理来计算。

解:C;
多元函数的连续性、可微性、偏导数是否存在

解: B;
多元函数的隐函数微分法

解:B;极小值$\to y’(x_0)=0,y’’(x_0)>0$
二重积分结合反函数

解:
基础过关一阶-线性代数
填空题
求抽象矩阵的逆

解: 思维要发散、灵活
将矩阵关系转化为线性方程组关系来求特定矩阵
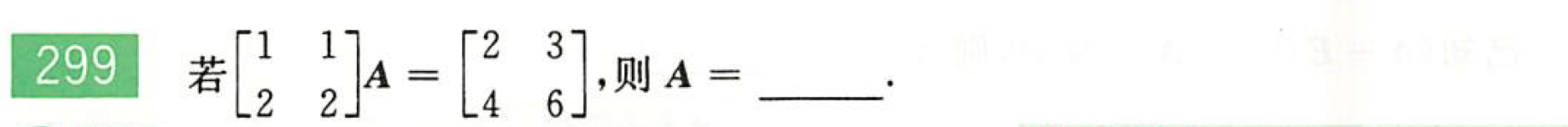
解:矩阵不可逆,所以不能用两边同乘逆矩阵求解。
故由$A=\left[\begin{matrix}2-t&3-u\\t&u \end{matrix}\right]$
求两矩阵运算后得到的矩阵的秩
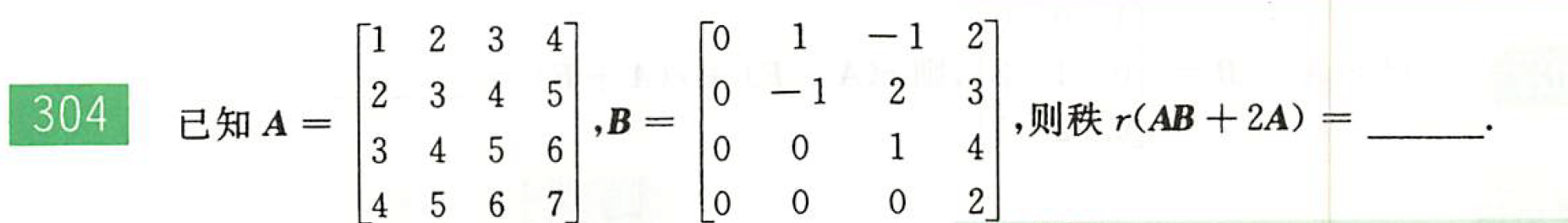
解:用到的定理:$A$可逆,则$r(AB)=r(BA)=r(B)$。故由$B+2E$可逆得$r(AB+2A)=r(A)=2$
由向量组之间的关系求矩阵的秩
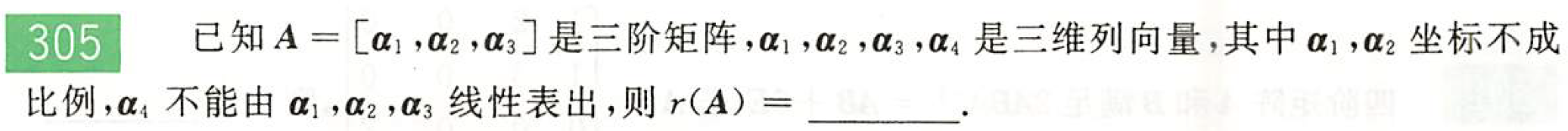
解: $\alpha_1,\alpha_2$坐标不成比例→$\alpha_1,\alpha_2$线性无关$\to 2\le r(A)\le 3$
由$\alpha_4$不能由$\alpha_1,\alpha_2,\alpha_3$线性表出可推出:
①. $x_1\alpha_1+x_2\alpha_2+x_3\alpha_3=\alpha_4$无解$\to r(\bar A)=r(A)+1\to r(A)\ne 3\to r(A)=2$
②. 因为$n+1$个$n$维向量必线性相关,故存在$k_i$不全为$0$,使得$k_1\alpha_1+k_2\alpha_2+k_3\alpha_3+k_4\alpha_4=0$,又因$\alpha_4$不能由$\alpha_1,\alpha_2,\alpha_3$线性表出可推出,则由$k_4=0$,则$k_1,k_2,k_3$不全为$0$,则$r(A)<3,r(A)=2$
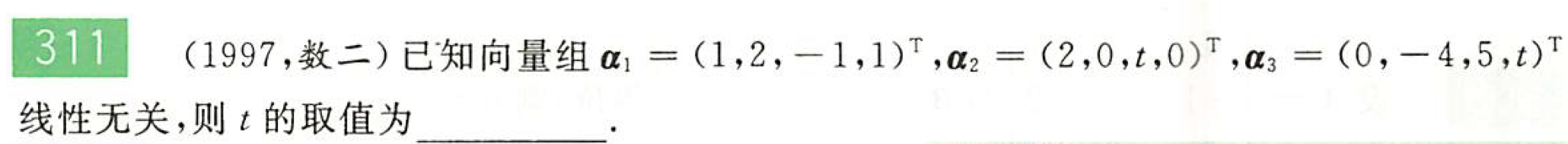 解: $\alpha_1,\alpha_2,\alpha_3$线性无关$\to r(\alpha_1,\alpha_2,\alpha_3)=3$
解: $\alpha_1,\alpha_2,\alpha_3$线性无关$\to r(\alpha_1,\alpha_2,\alpha_3)=3$
故$\forall t$,均有$r(\alpha_1,\alpha_2,\alpha_3)=3$
选择题
一个秩为r的向量组r+1或r-1个向量是否线性相关
 解:D
解:D
$\alpha_1,\alpha_2…\alpha_s$秩为$r\Leftrightarrow \alpha_1,\alpha_2…\alpha_s$的极大线性无关组有$r$向量
$\Leftrightarrow \alpha_1,\alpha_2…\alpha_s$中存在$r$个向量线性无关而$r+1$个向量必线性相关
向量组中任r-1个向量不一定都线性相关
矩阵转置的特征值和特征向量

解:D;重点看A,$A^T$和$A$有相同的特征值,但特征向量不同。
矩阵运算得到二次型
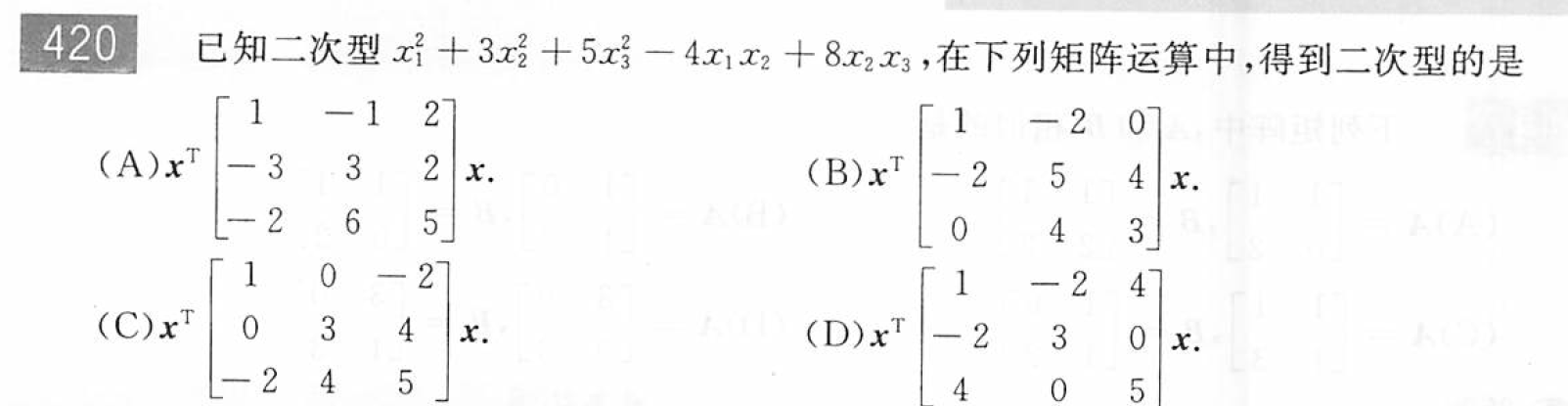
解:A;BCD虽都是对称的,但和二次型不匹配。A中矩阵不是对称矩阵,也就不是二次型的矩阵表示(二次型矩阵一定是对称矩阵),但直接计算可以得到和二次型相同的形式。
基础线性过关一阶-概率论
填空题

解: 服从几何分布,这里需注意“至少生产3件产品”包括最后的不合格品。
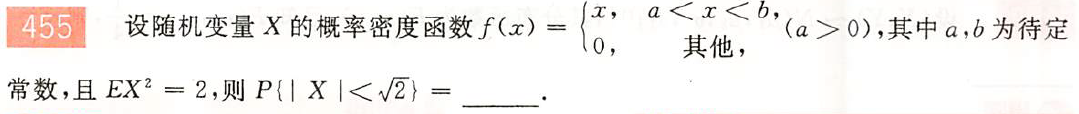
解: 从两个条件来求出$a,b$:①. $EX^2=\int_{a}^b x^2f(x)=2$;②. 规范性:$\int_{-\infty}^{+\infty}f(x)dx=1$,可求得$a=1,b=\sqrt3$

解:$Z=X_1-X_2\sim N(0,1)$,$D(|Z|)=E(Z^2)-(E|Z|)^2$
$D(|Z|)=D(Z)+[E(Z)]^2-(E|Z|)^2=1-\frac2\pi$
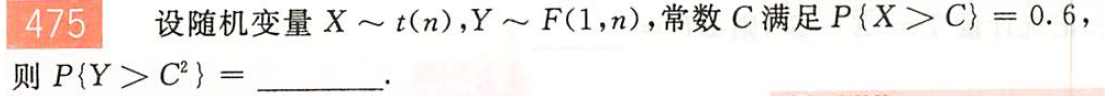
解: 重点注意:$P\{X>C\}=0.6\to C<0$

解:
要使$L(\theta)$最大,须满足$\theta$最小,又因$x_i\le \theta$,则$\theta=max\{x_i\}=x_{(n)}$
选择题
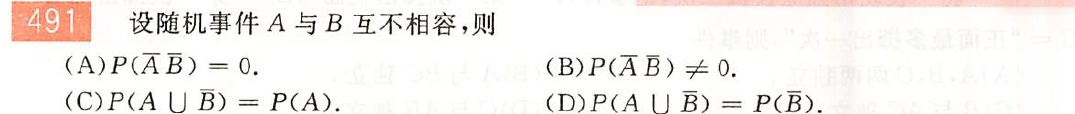 解: $D$;$A,B$互不相容$\Leftrightarrow P(AB)=0$,无法确定$P(\bar A\bar B)$的值。
解: $D$;$A,B$互不相容$\Leftrightarrow P(AB)=0$,无法确定$P(\bar A\bar B)$的值。

解: $F(x)$是单调不减的非负函数,故$F(x)$非奇非偶。
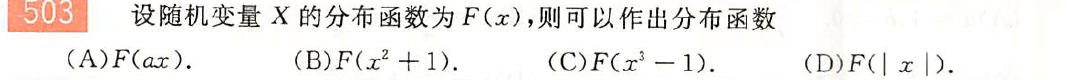
解: $C$;分布函数的性质:单调不减,非负有界,右连续。
- $A$:$a<0$时,三个性质都不满足
- $B$:$\lim_{x\to -\infty}F(x^2+1)\ne 0$
- $D$:$\lim_{x\to-\infty}F(|x|)\ne 0$
 解: $D$;二维正态分布函数的形式为:
解: $D$;二维正态分布函数的形式为:
可以看出$f(x,y)$不满足二维正态分布的形式,不服从二维正态。
则$f_X(x)\sim N(0,1)$,$f_Y(y)$同理。

解: $C$;

解: $B$;
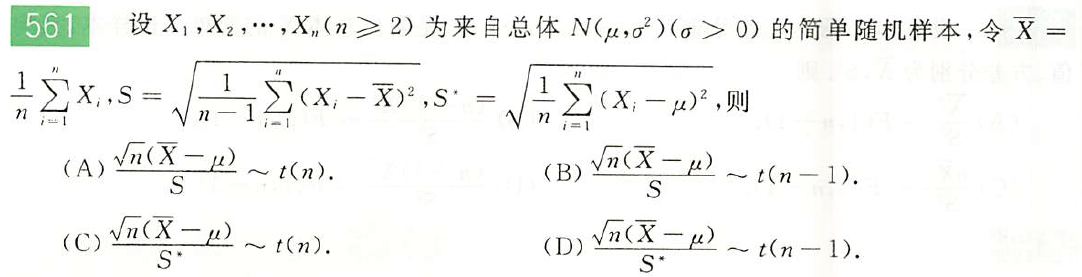
解: $B$;$B$显然正确。
$X,Y$不一定独立,所以$C,D$都不一定对。
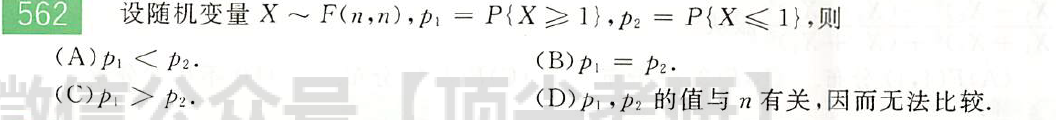
解: $B$;$X\sim F(n,n)\Leftrightarrow \frac1X\sim F(n,n)$

解: $A$;
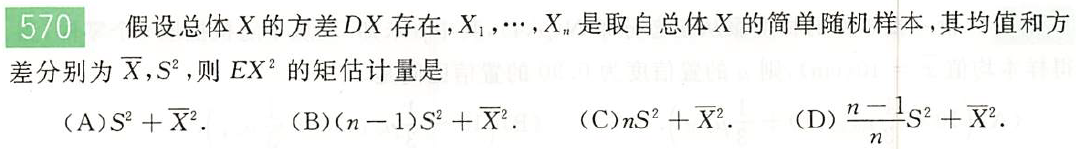
解: $D$;
$D(X)$的矩估计量为$\frac1n\sum_{i=0}^n(X_i-\bar X)^2$
或:

解: $C$;均值$\mu$是一个客观存在的数,所以说“总体均值$\mu$的真值以95%的概率落入区间$(\hat\theta_1,\hat\theta_2)$”不恰当。
基础过关二阶-高等数学
填空题

解: 前提:级数收敛$\Leftrightarrow$部分和有极限。
①.
②.
③.
④.
 解: $\sum_{n=1}^\infty (-1)^{n-1}a_n$收敛,$\sum_{n=1}^\infty a_n$发散$\Rightarrow$ $\sum_{n=1}^\infty (-1)^{n-1}a_n$条件收敛。即幂级数$\sum_{n=1}^\infty a_n t^n$在$t=-1$处条件收敛,即该收敛半径为$1$,令$t=2x^2$可得题目中所给的幂级数,则有$|2x^2|<1$,得收敛区间为$(-\frac1{\sqrt2},\frac1{\sqrt2})$。
解: $\sum_{n=1}^\infty (-1)^{n-1}a_n$收敛,$\sum_{n=1}^\infty a_n$发散$\Rightarrow$ $\sum_{n=1}^\infty (-1)^{n-1}a_n$条件收敛。即幂级数$\sum_{n=1}^\infty a_n t^n$在$t=-1$处条件收敛,即该收敛半径为$1$,令$t=2x^2$可得题目中所给的幂级数,则有$|2x^2|<1$,得收敛区间为$(-\frac1{\sqrt2},\frac1{\sqrt2})$。
又因$x=\pm\frac{1}{\sqrt2}$时$\sum_{n=1}^\infty a_n2^nx^{2n}=\sum_{n=1}^{\infty}a_n$发散,故收敛域为$(-\frac1{\sqrt2},\frac1{\sqrt2})$。

解:
当$x=4$时,幂级数成为$\sum_{n=1}^{\infty}\frac{1}{n[1+(-3/4)^n]}$
当$x=-4$时,幂级数成为$\sum_{n=1}^{\infty}\frac{(-1)^n}{n[1+(-3/4)^n]}=\sum_{n=1}^{\infty}\frac{(-1)^n}{n}-\sum_{n=1}^\infty \frac{(3/4)^n}{n[1+(-3/4)^n]}$
故收敛域为$[-4,4)$
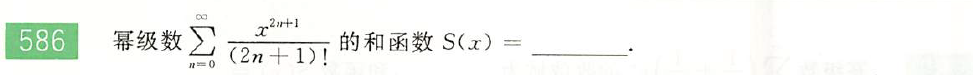
解: 用递推法,
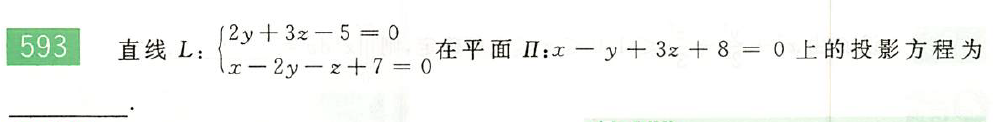
解: 求一直线在另一平面上的投影直线方程,思路:求出过直线$L$的与平面垂直的平面,并将两平面联立。
先求$L$的方向向量:
因为过直线$L$的平面与直线$L$的方向向量和平面$II$的法向量都平行,即且任取直线上$L$一点$(0,4,-1)$,则可得所求平面方程:
联立可得投影直线方程:

解: 思路:利用旋转后的点离坐标轴的距离不变来求解。
$M_0(x_0,y_0,z_0)$是$L$上一点,绕直线$L_1$旋转到$M(x,y,z)$,则有:
接下来可由直线方程$L$中$x_0,y_0,z_0$的关系以及$z=z_0$最终解出曲面方程为:
选择题

解: 举反例。
$B$:$u_n=\frac1{n^2},v_n=1$
$C$:$u_n=\frac1n-\frac1{n^2}$
$D$:$u_n=(-1)^n/n,v_n=-1/n$
证明$A$正确:$2|u_n v_n|\le u_n^2+v_n^2$,则$\sum_{n=1}^\infty |u_nv_n|$收敛,$\sum_{n=1}^\infty u_nv_n$收敛,故$\sum_{n=1}^\infty (u_n+v_n)^2=\sum_{n=1}^\infty (u_n^2+2u_nv_n+v_n^2)$收敛。

解:
则$\sum_{n=0}^\infty v_n=2u_{2n-1}+(u_{2n-1}-u_{2n})$发散。

解:举反例:
①. $a_n=(-1)^n/\sqrt n$
②. $a_n=(-1)^n/\sqrt n,b_n=(-1)^n/\sqrt n+1/n$
③. $a_n=(-1)^n/n$
证明④正确:$\sum_{n=1}^\infty a_n$收敛$\to \exists M,|a_n|\le M\to|a_nb_n|\le|Mb_n|\to$由$\sum_{n=1}^\infty a_n$绝对收敛,可得$\sum_{n=1}^\infty a_nb_n$绝对收敛。
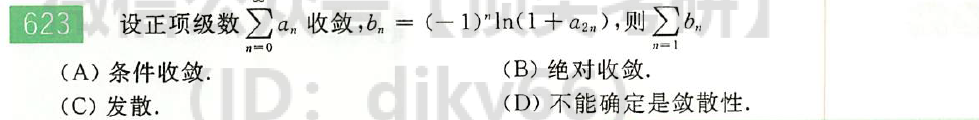
解: $\sum_{n=1}^\infty a_n$收敛$\to \lim_{n\to\infty}a_n=0\to \ln(1+a_{2n})\sim a_{2n}\to \sum_{n=1}^\infty b_n$绝对收敛。

解:
故②绝对收敛。

解: 因为$\lim_{n\to \infty}\frac{(\ln n)^2}{n}=0,(\ln n)^2\le n\to (\ln \ln n)^2\le \ln n$
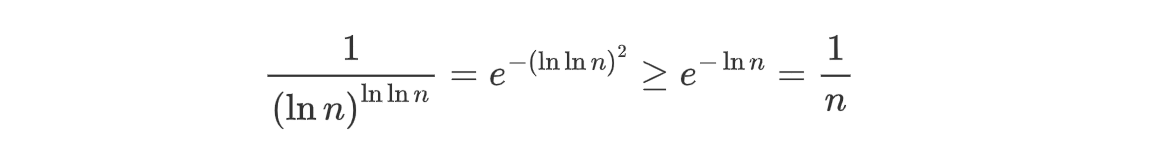
故发散。
 解:
解:
其中$\cos(\vec n,x),\cos(\vec n,y)$是法向量的方向余弦。设$\vec\tau$是$L$的沿逆时针方向的切线向量,则
则:

解: 用平面束方程法。
过点$(1,0,0),(0,1,0)$的直线方程为$\frac{x-1}1=\frac{y}{-1}=\frac z0$
即
过该直线的平面束方程为:$\lambda (x+y-1)+z=0$,即
法线向量为$(\lambda,\lambda,1)$.
曲面$z=x^2+y^2$在点$(x,y,z)$处的法向量为$\vec n_2=(2x,2y,-1)$,则
即$x=y=-\lambda/2$,代入平面束方程以及$z^2=x^2+y^2$得:
可得$\lambda_1=0,\lambda_2=-2$,代入到平面束方程得: