数一线代 李永乐线代讲义-典题错题

第一章 行列式

分块矩阵 拉普拉斯展开式

思路：把这个矩阵通过矩阵运算转化成可以利用拉普拉斯展开的形式。

$$\left[\begin{matrix} E&E\\0&E \end{matrix}\right] \left[\begin{matrix} A&B\\B&A \end{matrix}\right] \left[\begin{matrix} E&-E\\0&E \end{matrix}\right]= \left[\begin{matrix} A+B&0\\B&A-B \end{matrix}\right]$$

代数余子式求和

思路：因为$A_{ij}$与元素$a_{ij}$的大小无关，可构造一个行列式，用$A_{ij}$的系数置换$|A|$第三行的元素。

$$A_{31}+2A_{32}+A_{34}=|B|=\left[\begin{matrix} 1&1&2&-1\\-2&3&4&1\\\pmb1&\pmb2&\pmb0&\pmb1\\-4&2&0&6 \end{matrix}\right]$$

第二章：矩阵

计算矩阵的幂次方

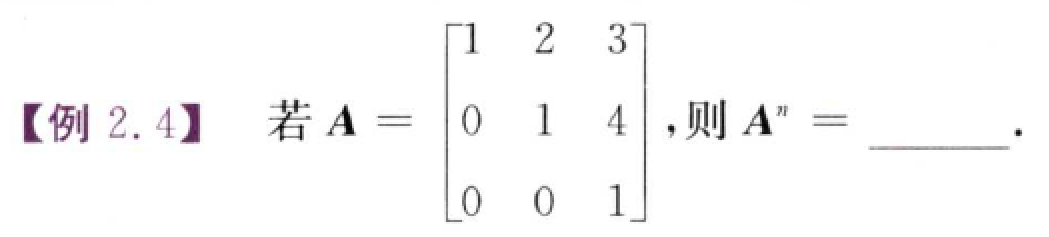
思路：将矩阵转变为一个单位矩阵$A$和另一个矩阵的和$B$，$(E+B)^n=C_n^mE^{n-m}B^m$

可以算出当$n\gt 2$时，$B^n=0$

思路：

①. 分块矩阵公式：$\left[\begin{matrix}B&O\\O&C\end{matrix}\right]^n=\left[\begin{matrix}B^n&O\\O&C^n\end{matrix}\right]$

②. 求$B^n$，思路同例2.4

③. 求$C^n$，$r(C)=1$，则$\exists$列向量$ \alpha,\beta,C=\alpha \beta^T,C^n=(\beta^T\alpha)^{n-1}C$

分块矩阵求逆

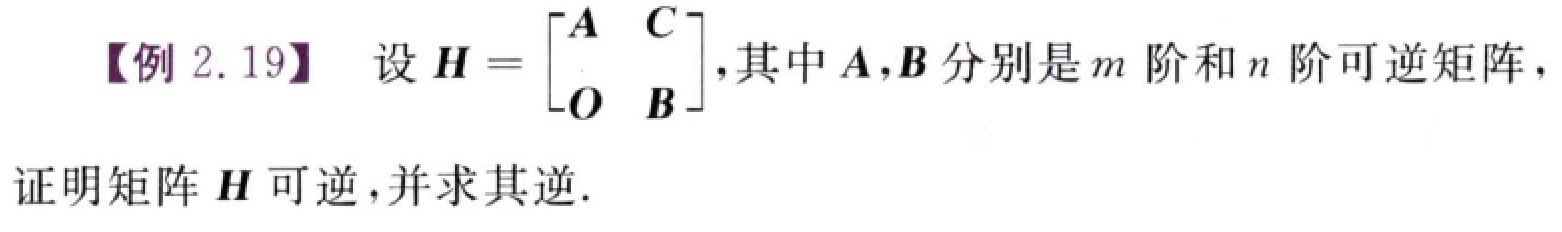
思路：设$H^{-1}=\left[\begin{matrix}X&Y\\Z&W\end{matrix}\right]$，通过$HH^{-1}=E$列出方程组求解$X,Y,Z,W$

正交矩阵的证明题

思路：利用正交矩阵的性质$A^TA=E,|A|=\pm 1$

由$|A|+|B|=0$得，$|A|=-|B|$

$$\begin{aligned} |A+B|&=|(BB^T)A+B(A^TA)|\\ &=|B||B^T+A^T||A|\\ &=-|B|^2|(A+B)^T|\\ &=-|A+B| \end{aligned}$$

第三章：n维向量

线性无关的证明（痛点）

思路：用定义法证明，先设$k_1\alpha_1+k_2\alpha_2+…+k_m\alpha_m=0$，然后通过题目所给条件得出$k_i=0$

$$k_1\alpha+k_2A\alpha+...+k_mA^{m-1}\alpha_m=0$$

上式两端左乘$A^{m-1}$，得$k_1A^{m-1}\alpha=0$，从而有$k_1=0$；

然后再左乘$A^{m-2}、A^{m-3}….$得到$k_2\sim k_m=0$

思路：定义法，设

$$k_1\alpha_1+k_2\alpha_2+k_3\alpha_3=0$$

由所给条件可得，$(A-E)\alpha_1\ne0,(A-E)\alpha_2=\alpha_1,(A-E)\alpha_3=\alpha_2$

两边三次同乘$A-E$

本题很像讨论秩的情况，但实际上无法通过秩来解此题，要及时转变思路。

线性表出的证明（有点更痛的点）

思路：通过线性表出和线性相关的关系性质，整体组与部分组、延伸组的关系来解题（详见线代第三章博客），或通过定义、秩来解题

（1）

法一：$\alpha_2,\alpha_3,\alpha_4$线性无关→$\alpha_2,\alpha_3$线性无关

$\alpha_1,\alpha_2,\alpha_3$线性相关，$\alpha_2,\alpha_3$线性无关→$\alpha_1$可由$\alpha_2,\alpha_3$唯一线性表出。

法二：从定义出发，反证法

（2）法一：定义，反证法

假设可以，则有

$$\alpha_4=k_1\alpha_1+k_2\alpha_2+k_3\alpha_3$$

又因$\alpha_1$可由$\alpha_2,\alpha_3$线性表出，$\alpha_1=m_2\alpha_2+m_3\alpha_3$，代入上式得

$$\alpha_4=(k_1m_2+k_2)\alpha_2+(k_1m_3+k_3)\alpha_3$$

与$\alpha_2,\alpha_3,\alpha_4$矛盾，故不可以线性表出。

法二：利用矩阵和增广矩阵秩的关系

仍然假设可以，则有

$$k_1\alpha_1+k_2\alpha_2+k_3\alpha_3=\alpha_4$$

上式可看成一个非齐次线性方程组，

由$\alpha_1,\alpha_2,\alpha_3$线性相关可得齐次线性方程组有非零解，则$r(A)=r(\alpha_1,\alpha_2,\alpha_3)<3$

由$\alpha_2,\alpha_3,\alpha_4$线性无关可得$r(\overline A)=r(\alpha_1,\alpha_2,\alpha_3,\alpha_4)\ge 3$

$r(A)\ne r(\overline A)$，故非齐次线性方程组无解，不可以线性表出。

法一：用基本方法，定义，反证法证明，思路大体和上题相同，此处略

法二：看成线性方程组，讨论秩来证明

由$\beta$可由$\alpha_1\sim\alpha_m$线性表出，则非齐次线性方程组$x_1\alpha_1+…+x_m\alpha_m=\beta$有解，则$r(\alpha_1,…,\alpha_m)=r(\alpha_1,…,\alpha_m,\beta)$

由$\beta$不能由$\alpha_1,…\alpha_{m-1}$线性表出，则非齐次线性方程组$x_1\alpha_1+…+x_{m-1}\alpha_{m-1}=\beta$，则$r(\alpha_1,…,\alpha_{m-1})+1=r(\alpha_1,…,\alpha_{m-1},\beta)$

考察：$x_1\alpha_1+x_2\alpha_2+…+x_{m-1}\alpha_{m-1}=\alpha_m$

$$\begin{aligned} r(\alpha_1,...,\alpha_m)&\le r(\alpha_1,...,\alpha_{m-1})+1 \\ &=r(\alpha_1,...,\alpha_{m-1},\beta)\\ &\le r(\alpha_1,...,\alpha_{m-1},\alpha_{m},\beta)\\ &=r(\alpha_1,...,\alpha_m) \end{aligned}$$

故$r(\alpha_1,…,\alpha_{m-1})+1=r(\alpha_1,…,\alpha_{m})$，$\alpha_m$不能由$\alpha_1,…,\alpha_{m-1}$线性表出；$r(\alpha_1,…,\alpha_{m-1},\beta)=r(\alpha_1,…,\alpha_{m-1},\beta,\alpha_m)$，$\alpha_m$可由$\alpha_1,…,\alpha_{m-1},\beta$线性表出，

分块矩阵的秩的比较（举反例）

思路：$A=\left[\begin{matrix}1&0\\0&0\end{matrix}\right],B=\left[\begin{matrix}1&0\\1&0\end{matrix}\right]$

思路：$A=\left[\begin{matrix}0&1\\0&0\end{matrix}\right],B=\left[\begin{matrix}0&1\\1&0\end{matrix}\right]$

第四章：线性方程组

和线性表出联系

思路：由$\alpha_1,\alpha_2,\alpha_3$可由$\beta_1,\beta_2,\beta_3$线性表出，则有：

$$\begin{cases} \alpha_1=a_{11}\beta_1+a_{12}\beta_2+a_{13}\beta_3\\ \alpha_2=a_{21}\beta_1+a_{22}\beta_2+a_{23}\beta_3\\ \alpha_3=a_{31}\beta_1+a_{32}\beta_2+a_{33}\beta_3\\ \end{cases}$$ $$[\alpha_1,\alpha_2,\alpha_3]=[\beta_1,\beta_2,\beta_3] \left[\begin{matrix} a_{11}&a_{21}&a_{31}\\ a_{12}&a_{22}&a_{32}\\ a_{13}&a_{23}&a_{33}\\ \end{matrix}\right]\Rightarrow A=BC\Rightarrow A^T=C^TB^T$$

故$A^Tx=C^TB^Tx=0$，选D

证明向量组是基础解系

思路：要证$\alpha_1,\alpha_2,…,\alpha_t$是$Ax=0$的基础解系，需要：

• 验证$\alpha_1,\alpha_2,…,\alpha_t$是$Ax=0$的解
• 证明$\alpha_1,\alpha_2,…,\alpha_t$线性无关
• $t=n-r(A)$

前两步略，第三步，$Ax=0$已经有了两个解，说明$r(A)\le1 $，又因$A$是非零矩阵，则$r(A)\ge1$，故$r(A)=1,n-r(A)=2$

通过n阶非零子式判断秩

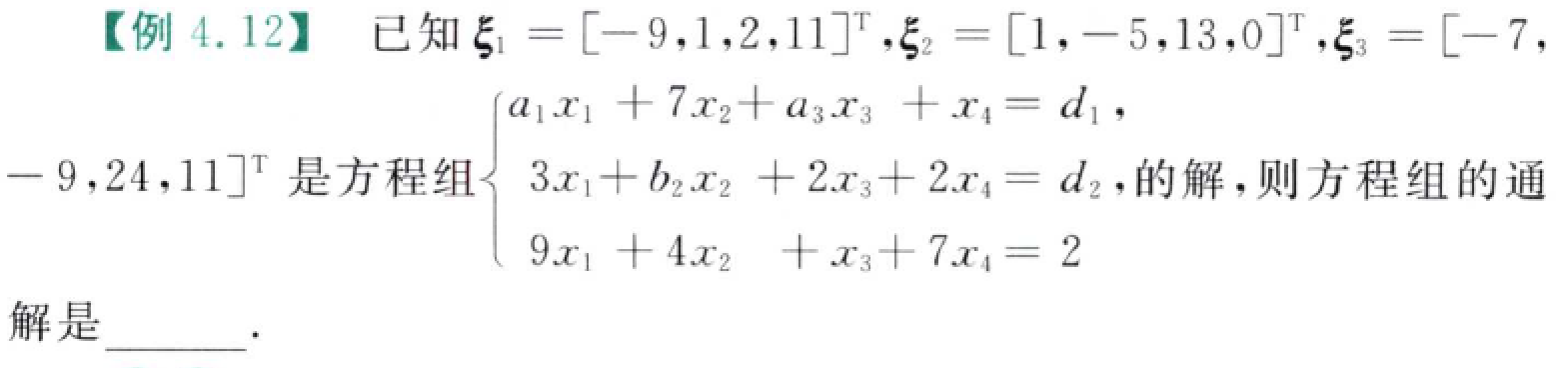
思路：需要关注的点是，方程组对应的矩阵$A$存在2阶非零子式$\begin{vmatrix}2&2\\1&7 \end{vmatrix}\ne 0$，可以得出结论：$r(A)\ge 2$

齐次和非齐次解的判定

思路：此题切忌用克拉默法则考虑， 克拉默法则的前提是$n$个方程$n$个未知量的方程组；需要利用$r(A)$和$r(\overline A)$的值以及它们的大小关系来求解。

（A）$A$不一定是$n$阶矩阵，行列式可能不存在

（B）$r(A)=n\nRightarrow r(A)=r(\bar A)=n$

（C）$r(A)\lt n\nRightarrow r(A)=r(\bar A)\lt n$

（D）$r(A)=r(\bar A)<n\Rightarrow r(A)<n$

和线性相关联系

思路：$r(A)\le r(\bar A)\le m$，当$A$的行向量线性无关时，$r(A)=m=r(\bar A)$

关于为什么没有考虑$n$，这是因为如果$A$的行向量线性无关，一定是满足$r(A)=m$，而如果$m>n$时，$r(A)\le n\lt m$，此时方程组一定线性相关。相关的一些思考

思路：$A$的行向量线性无关，则$r(A)=r(A^T)=r(A^TA)=4$，$A:4×5$，$A^T: 5×4$，$A^TA: 5×5$

（A）$r(A^T)=4=n$→只有非零解

（B）$r(A^TA)=4<n=5$→必有非零解

（C）因为$r(A)\le r(\bar A)\le 4$，若$r(A)=4$，则$r(A)=r(\bar A)=4<n=5$→必有无穷多解

（D）因为$r(A^T)\le r(\bar A^T)\le 5$，若$r(A^T)=4$，当$r(\bar A^T)=4$时，$r(A^T)=r(\bar A^T)=4$有唯一解；当$r(\bar A^T)=5$时，无解。D错误

D选项书中给的答案意思是，4个线性无关的五维向量不可以表示所有的5维向量，所以存在五维向量b，使得$A^Tx=b$无解。

方程组同解，内积

思路：分别从两边证明，注意“内积☆”的应用

①. 设$\alpha$是$Ax=0$的解，$A\alpha=0$，则$A^TA\alpha=A^T\cdot 0=0$

②. 设$\alpha$是$A^TAx=0$的解，则$A^TA\alpha=0$，等式两边左乘$\alpha^T$，得$\alpha^TA^TA\alpha=(A\alpha)^T(A\alpha)=||A\alpha||^2=0$，故$A\alpha=0$

第五章：特征值和特征向量

证明有相同特征值

思路：重要的$AA^{-1}=E$

$$(A^{-1}A)BA=A^{-1}(AB)A=BA$$

则$A,B$相似，有相同的特征值

$$\begin{aligned} |\lambda E-AB|&=|\lambda AA^{-1}-AB|\\ &=|A||\lambda A^{-1}-B|\\ &=|\lambda A^{-1}-B||A|\\ &=|\lambda E-BA| \end{aligned}$$

又有和内积有关的

思路：设$\alpha$为n维单位列向量，则$\alpha\alpha^T$的特征根为$1,0,….,0$。$A=\alpha\alpha^T,A^2=\alpha(\alpha^T\alpha)\alpha^T=\alpha\alpha^T=A$（$A^2=A$时求特征根，常见套路，$\lambda=0,1$）。因为$\alpha\alpha^T\alpha=\alpha(\alpha^T\alpha)=\alpha$，特征根$\lambda=1$对应的特征向量有一个$\alpha$，故$\lambda=1$为一重。

$E-\alpha\alpha^T$的特征值为$1,0,…,0$，相似对角化后发现$E-\alpha\alpha^T$不可逆。

和向量正交相关

思路：$\alpha_1,\alpha_2$正交$→ \alpha_1^T\alpha_2=0$

已知$A^T=A,A\alpha_1=\lambda_1\alpha_1,A\alpha_2=\lambda_2\alpha_2$

$$\alpha_2^TA\alpha_1=\lambda_1\alpha_2^T\alpha_1=\alpha_2^TA^T\alpha_1=(A\alpha_2)^T\alpha_1=(\lambda_2\alpha_2)^T\alpha_1=\lambda_2\alpha_2^T\alpha_1$$

故$(\lambda_1-\lambda_2)\alpha_2^T\alpha_1=0$，又因$\lambda_1\ne \lambda_2$，则$\alpha_2^T\alpha_1=0$

第六章：二次型

配方法化二次型不含平方项的情况

思路：首先令：

$$\begin{cases} x_1=y_1+y_2,\\ x_2=y_1-y_2,\\ x_3=\quad\quad\quad\ y_3, \end{cases}$$

可得$f(x_1,x_2,x_3)=2(y_1+y_3)^2-2(y_2-y_3)^2$

再令：

$$\begin{cases} z_1=y_1\quad\quad +y_3,\\ z_2=\quad \quad y_2 -y_3,\\ z_3=\quad\quad\quad\quad y_3, \end{cases}\Rightarrow \begin{cases} y_1=z_1\quad\quad -z_3,\\ y_2=\quad\quad z_2+z_3,\\ y_3=\quad\quad\quad\quad z_3, \end{cases}$$

最终得$f=2z_1^2-2z_2^2$

坐标变换矩阵求解

思路：

（1）由$g=(y_1+y_2)^2+4y_3^2$得$p=2,q=0$，则可写出二次型$f$的矩阵，求特征值来满足正负、惯性系数的要求，即可求得$a=-1/2$

（2）①. 先配方：$f=(x_1-\frac12x_2-\frac12x_3)^2+\frac34(x_2-x_3)^2$

②. 坐标转换为规范型（作为过渡），得到坐标转换矩阵

$$\begin{cases} z_1=x_1-\frac12x_2-\frac12x_3,\\ z_2=\quad\quad\frac{\sqrt 3}{2}x_2-\frac{\sqrt 3}{2}x_3,\\ z_3=\quad\quad\quad\quad \quad\quad x_3, \end{cases}\Rightarrow \left[\begin{matrix} x_1\\x_2\\x_3 \end{matrix}\right]= \left[\begin{matrix} 1&\frac1{\sqrt 3}&1\\ 0&\frac2{\sqrt 3}&1\\ 0&0&1 \end{matrix}\right] \left[\begin{matrix} z_1\\z_2\\z_3 \end{matrix}\right]$$

有$f=z_1^2+z_2^2$

③. 将规范型通过坐标转换为$g$，得到坐标转换矩阵

$$\begin{cases} z_1=y_1+y_2,\\ z_2=\quad\quad\quad\quad 2y_3,\\ z_3= \quad\quad y_2, \end{cases}\Rightarrow \left[\begin{matrix} z_1\\z_2\\z_3 \end{matrix}\right]= \left[\begin{matrix} 1&1&0\\ 0&0&2\\ 0&1&0 \end{matrix}\right] \left[\begin{matrix} y_1\\y_2\\y_3 \end{matrix}\right]$$

④. 最后的坐标变换矩阵$P$就是上面两次坐标变换矩阵的乘积。

关于正定的证明

思路：

①. 充分性：若$A=C^TC$，则$A^T=(C^TC)^T=C^TC=A,A$是对称阵。

$\forall x\ne 0,x^TAx=x^TC^TCx=(Cx)^TCx=||Cx||^2>0$，故$A$正定。

或：存在坐标变换$x=C^{-1}y$，有$x^TAx=y^T(C^T)^{-1}C^TCC^{-1}y=y_1^2+y_2^2+…y_n^2$

②. 必要性：已知对于任一个二次型，都可通过正交变换转换成规范型，故对于正定阵$A$，存在$x=C_1y,y=C_2z$，使得$x^TAx=y^TΛy=E$，则有$C_1^TAC_1=Λ,C_2^TΛC_2=E$，因为$C_1,C_2$可逆，所以可得到$A=(C_2^{-1}C_1^{-1})^T(C_2^{-1}C_1^{-1})=C^TC$

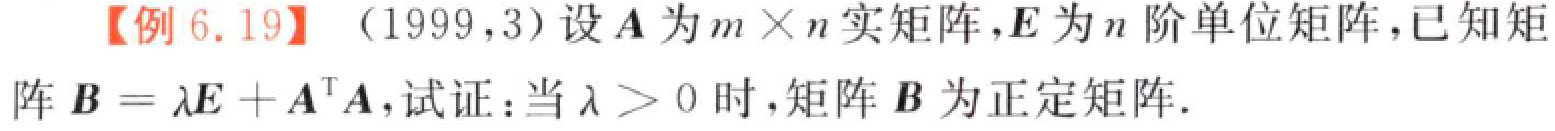
思路：从定义出发

$$x^TBx=\lambda x^Tx+(Ax)^T(Ax)=\lambda ||x||^2+||Ax||^2\gt 0\quad \forall x\ne0$$

思路：证明$A-B^2$是正定阵，从而有$|A-B^2|\ne 0$，可逆

$$(A-B^2)^T=A^T-(B^T)^2=A-(-B)^2=A-B^2$$

故是对称矩阵。

$$x^T(A-B^2)x=x^TAx+x^TB^TBx=x^TAx+||Bx||^2\gt 0$$

得证。

等价、相似、合同综合

思路：最基础且重要的不要忘记，对矩阵做一个初等行（列）变换相当于对矩阵左（右）乘一个初等矩阵。

初等变换矩阵等价。

$$\left[\begin{matrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end{matrix}\right]A \left[\begin{matrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end{matrix}\right]=B$$ $$\left[\begin{matrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end{matrix}\right]^{-1}A \left[\begin{matrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end{matrix}\right]^{-1}= \left[\begin{matrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end{matrix}\right]^TA \left[\begin{matrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end{matrix}\right]^T=B$$

故矩阵相似，合同。