数一 可导和导函数极限概念题专题
参考:【导数较难概念42结论】秒杀可导与导函数极限概念题【小元老师】数学_哔哩哔哩_bilibili
引出
首先要知道两个符号的区别:
- 第一行指的是$f(x)$在$x_0$点的左导数和右导数
- 第二行指的是$f(x)$的导函数$f’(x)$在$x_0$点的左极限和右极限
它们两个并不是一回事。比如下面两个函数在$x=0$的导数为$0$,但导函数不连续,$\lim_{x\to 0^-}f’(x),\lim_{x\to 0^+}f’(x)$都不存在($x=0$是$f’(x)$的振荡间断点):
$f’_-(x_0)\quad f’_+(x_0)$研究的函数在$x_0$这一点是可导的;$f’(x_0-0)\quad f’(x_0+0)$研究的是函数在$x_0$这一点附近的可导情况。
相关结论
导函数的间断点存在性问题
1、在一开区间上可导的函数$f(x)$的导函数没有第一类间断点。
2、设$f(x)$在$x=x_0$的邻域内有定义,$f(x)$在$x=x_0$的某去心邻域内可导,若$\lim_{x\to x_0}f’(x)=\infty$,则$f’(x_0)$不存在。(或,可导的函数,导函数不会出现无穷间断)。
3、若$f’(x_0)$存在,且导函数在$x_0$点不连续,则导函数$f’(x)$只可能在$x_0$处出现震荡间断。
4、导数极限定理:设$f(x)$在$U(x_0)$连续,$U^0(x_0)$可导,且极限$\lim_{x\to x_0}f’(x)$存在,则$f(x)$在点$x_0$可导,且$f’(x_0)=\lim_{x\to x_0}f’(x)$。(在结论1的基础上可以得到)
某点可导的情况
1、$f(x)$在$x_0$可导$\Rightarrow$:(可以推出)
- $f’(x)$在$x_0$有定义;(导数有定义)
- $f’_-(x_0)=f’_+(x_0)$;(左右导数存在且相等)
- $f(x)$在$x_0$连续。(可导必连续)
2、$f(x)$在$x_0$可导$\nRightarrow$:(不能推出)
- $f(x)$在$x_0$邻域内连续或可导;
- $f’(x)$在$x_0$点极限存在或连续。
反例:$D(x)=\begin{cases}1,&{x为有理数}\\0,&{x为无理数} \end{cases}$,$f(x)=x^2D(x)$在$x=0$处连续而且可导,但在$x\ne0$处不连续不可导;$f(x)=xD(x)$在$x=0$处连续而且不可导;在$x\ne 0$处不连续不可导。
3、$\lim_{x\to x_0^-}f’(x),\lim_{x\to x_0^+}f’(x)$至少有一个不存在$\nRightarrow$$f(x)$在$x_0$不可导(即仍然有可能可导)。
4、$f’(x_0)>0(<0)\nRightarrow f(x)$在$x_0$的邻域单增(单减);(即某点导数的正负决定不了邻域的单调性)
5、$\lim_{x\to x_0^-}f’(x),\lim_{x\to x_0^+}f’(x)$存在(包含相等的情况)$\nRightarrow$(不能推出$f(x)$)(与导函数的间断点存在性问题第一个相区别)
- $f(x)$在$x_0$处极限存在、连续、可导;
反例:$y=\begin{cases}2x,&{x>0}\\2x+5,&{x\le 0} \end{cases}$
某邻域可导的情况
1、$f(x)$在$x_0$某邻域$U_\delta(x_0)$内可导$\Rightarrow$
- $f(x)$在$U_\delta(x_0)$内有定义、连续、极限存在;
- $f’(x)$在$U_\delta(x_0)$内有定义。
2、$f(x)$在$x_0$某邻域$U_\delta(x_0)$内可导$\nRightarrow$
- $f’(x)$在$U_\delta(x_0)$内连续、极限存在;
- $f’(x)$在$x_0$点极限存在。
反例:开头提到的函数。
某去心邻域内可导的情况
1、$f(x)$在$x_0$去心邻域$\dot U_\delta(x_0)$内可导$\Rightarrow$
- $f’(x)$在$\dot U_\delta(x_0)$内有定义;
- $f(x)$在$\dot U_\delta(x_0)$内有定义、极限存在、连续。
2、$f(x)$在$x_0$去心邻域$\dot U_\delta(x_0)$内可导$\nRightarrow$
$f(x)$在$x_0$点有定义、极限存在、连续、可导;
$f’(x)$在$x_0$点有定义。
某点连续
1、$f(x)$在$x_0$连续$\Rightarrow f(x)$在$x_0$邻域内有定义;
2、$f(x)$在$x_0$连续$\nRightarrow $
- $f(x)$在$x_0$邻域内连续;
- $f(x)$在$x_0$可导。
某邻域内连续
1、$f(x)$在$x_0$某邻域$U_\delta(x_0)$内连续$\Rightarrow$ $f(x)$在$x_0$邻域$U_\delta(x_0)$内有定义
2、$f(x)$在$x_0$某邻域$U_\delta(x_0)$内连续$\nRightarrow f(x)$在$x_0$可导或$f(x)$在邻域内某点可导(魏尔斯特拉斯函数)
常用反例(结论太多不好记,通过记反例更容易)
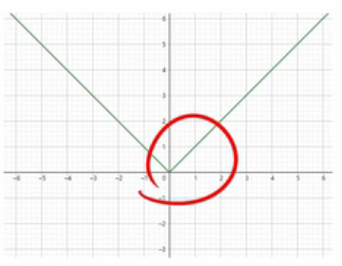
1、$y=|x|$:在$x=0$处连续但极限不存在、函数不可导、导函数不连续,左右导函数极限不相等。
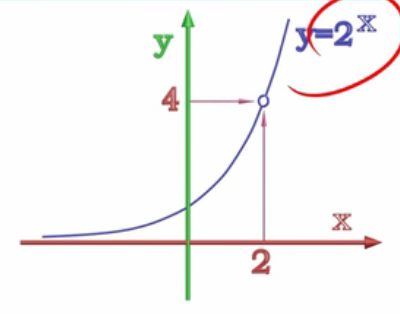
2、$y=2^x$(挖去$(2,4)$这个点):有一个可去间断点,在$x=2$不连续,在去心邻域上可导,左右导函数极限相等。
3、$y=\begin{cases}2x,&{x>0}\\2x+5,&{x\le 0} \end{cases}$:有一个跳跃间断点,在$x=0$处不连续、导数不存在,但导函数在$x=0$处的左右极限相等。
4、$D(x)=\begin{cases}1,&{x为有理数}\\0,&{x为无理数} \end{cases}$,$f(x)=x^2D(x)$在$x=0$处连续而且可导,但在$x\ne0$处不连续不可导;$f(x)=xD(x)$在$x=0$处连续而且不可导;在$x\ne 0$处不连续不可导。
5、下面两个函数在$x=0$的导数为$0$,但导函数不连续,左右导函数极限$\lim_{x\to 0^-}f’(x),\lim_{x\to 0^+}f’(x)$都不存在($x=0$是$f’(x)$的振荡间断点):



