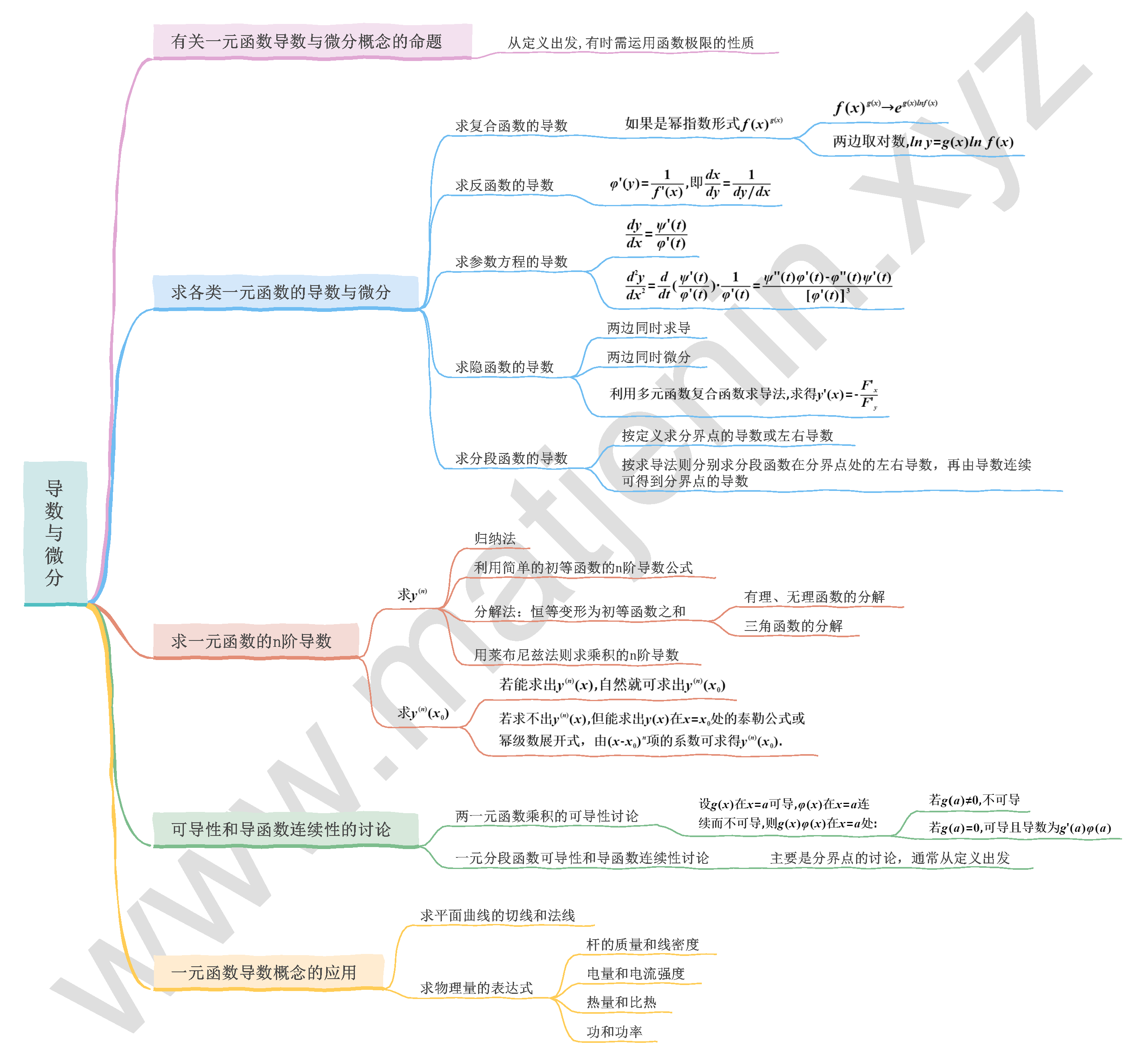
数一高数第二章：导数与微分

一、导数与微分的概念

1. 导数的概念

定义：设函数$y=f(x)$在$x_0$的某邻域内有定义，如果极限

$\lim_{△x→0}\frac{△y}{△x}=\lim_{△x→0}\frac{f(x_0+△x)-f(x_0)}{△x}$

存在，则称$f(x)$在点$x_0$处可导，此极限值为$f(x)$在$x_0$处的导数。

等价形式：
$f'(x_0)=\lim_{x→x_0}\frac{f(x)-f(x_0)}{x-x_0}=\lim_{h→0}\frac{f(x_0+h)-f(x_0)}{h}$

左导数，右导数

函数$f(x)$在点$x_0$处可导的充要条件是在该点处左导数与右导数都存在且相等。

2. 微分的概念

定义：设函数$y=f(x)$在点$x_0$的某一邻域内有定义，如果函数的增量$△y=f(x_0+△x)-f(x_0)$可以表示为：

$△y=A△x+o(△x),(△x→0)$

其中$A$为不依赖与$△x$的常数，则称函数$f(x)$在点$x_0$处可微， $A△x$为函数$f(x)$在点$x_0$处相应与自变量增量$△x$的微分，$dy=A△x$

定理：可微和可导互为充要条件。

$dy=f'(x_0)△x=f'(x_0)dx$

若$f(x)$在点$x_0$处可微，则在点$(x_0,y_0)$附近可以用切线段近似代替曲线段。

3. 导数和微分的几何意义

导数的几何意义：斜率。

在一点上可导，此点上必有切线存在，反之不一定，例如$y=x^{\frac13}$在$(0,0)$处。

微分的几何意义：切线上的增量。

4. 连续、可导、可微之间的关系

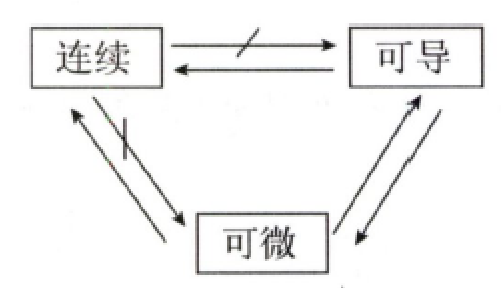
由逆否命题知，函数不连续→不可导、不可微

强化：函数在$x=x_0$处可导，则函数在$x=x_0$处连续，但在$x=x_0$的某一邻域内不一定连续，因为这样需要保证在此邻域内的点处处可导，反例：
$f(x)=\begin{cases} x&,{x为有理数}\\ 0&,{x为无理数} \end{cases}$
此函数仅在$x=0$处连续。

二、导数公式及求导法则

1. 基本求导公式

$(\log_ax)'=\frac{1}{x\ln a}(a>0,a≠1)$ $(arcsin x)'=\frac{1}{\sqrt{1-x^2}} \quad (arccosx)'=-\frac{1}{\sqrt{1-x^2}}$ $(arctan x)'=\frac{1}{1+x^2} \quad (arccotx)'=-\frac{1}{1+x^2}$ $(tanx)'=sec^2x \quad (cotx)'=-csc^2x$ $(secx)'=secx·tanx \quad (csc x)'=-csc x ·cotx$ $[ln(x+\sqrt{x^2+1})]'=\frac{1}{\sqrt{x^2+1}} \quad [ln(x+\sqrt{x^2-1})]'=\frac{1}{\sqrt{x^2-1}}$

2. 隐函数求导法

从方程两边对$x$求导，可得到一个含有$y’$的方程，从中解出$y’$

3. 反函数求导法

设$y=f(x)$可导，且$f’(x)\ne 0$，则存在反函数$x=\varphi(y)$，且

$\varphi'(y)=\frac1{f'(x)} \quad 即\frac{dx}{dy}=\frac1{\frac{dy}{dx}}$

4. 参数方程求导法

$\begin{cases} x=\varphi(t)\\ y=ψ(t) \end{cases} ,(\alpha<t<\beta)$

$\varphi’(t)\ne 0$，则

$\frac{dy}{dx}=\frac{ψ'(t)}{\varphi'(t)}$ $\frac{d^2y}{dx^2}=\frac{d}{dt}(\frac{ψ'(t)}{\varphi'(t)})·\frac1{\varphi'(t)}=\frac{ψ''(t)\varphi'(t)-\varphi''(t)ψ'(t)}{[\varphi'(t)]^3}$

5. 对数求导法

对于多项相乘、相除、开放、乘方的式子，一般先取对数再求导。（或化成指数）

6. 变限积分求导公式

设$F(x)=\int^{\varphi_2(t)}_{\varphi_1(t)}f(t)dt$，其中$f(x)$在$[a,b]$上连续，可导函数$\varphi_1(x)$和$\varphi_2(x)$的值域在$[a,b]$上，则在函数$\varphi_1(x)$和$\varphi_2(x)$的公共定义域上，有

$F'(x)=\frac{d}{dx}[\int^{\varphi_2(x)}_{\varphi_1(x)}f(t)dt]=f[\varphi_2(x)]\varphi'_2(x)-f[\varphi_1(x)]\varphi'_1(x)$

三、高阶导数

定义式：

$\begin{aligned} f^{(n)}(x_0)&=\lim_{△x→0}\frac{f^{(n-1)}(x_0+△x)-f^{(n-1)}(x_0)}{△x}\\ &=\lim_{x→x_0}\frac{f^{(n-1)}(x)-f^{(n-1)}(x_0)}{x-x_0} \end{aligned}$

莱布尼茨公式：

$(uv)^{(n)}=\sum_{k=0}^nC_n^ku^{(k)}v^{(n-k)}$

常见函数的高阶导数：

$(sinkx)^{(n)}=k^nsin(kx+n·\frac{π}{2}) \quad (coskx)^{(n)}=k^ncos(kx+n·\fracπ2)$ $(lnx)^{(n)}=(-1)^{n-1}\frac{(n-1)!}{x^n}(x>0)$ $(\frac1x)^{(n)}=(-1)^n\frac{n!}{x^{n+1}},n=1,2,...$

技巧知识点

①. 若$x∈(x_0-\delta,x_0+\delta),x\ne x_0$时$f(x)=g(x)$，则$f(x)$与$g(x)$在$x=x_0$处不一定具有相同的可导性。例如：

$f(x)=x^2\quad\quad g(x)=\begin{cases} x^2&,{x\ne0}\\ 1&,{x=0} \end{cases}$

②.$n$为奇数时，$x^n+1=(x+1)(x^{n-1}-x^{n-2}+…-x+1)$

$n$为偶数时，$x^n-1=(x+1)(x^{n-1}-x^{n-2}+…+x-1)$

$x^3+1=(x+1)(x^2-x+1)\quad \quad \quad x^3-1=(x-1)(x^2+x+1)$

③. （李正元P47 例2.23、24）设$g(x)$在$x=a$可导，$\varphi(x)$在$x=a$连续而不可导，则$g(x)\varphi(x)$在$x=a$处：

$\begin{cases} 不可导&，{若g(a)\ne 0}\\ 可导且导数为g'(a)\varphi(a)&，{若g(a)=0} \end{cases}$

④. 设$f(x)$在$x=0$处连续，则$\lim_{x\to 0}\frac{f(x)-f(-x)}{2x}=0$存在不能说明$f(x)$在$x=0$处可导，例子：$f(x)=|x|$；$\lim_{x\to \infty}xf(\frac1x)$可以说明$f(x)$在$x=0$处可导，且满足$f(0)=0$

⑤. 平面曲线$C$的参数方程为：$\begin{cases}x=x(t)\\y=y(t) \end{cases}(\alpha\le t\le\beta)$，则曲线$C$在点$M_0(x_0,y_0)((x_0,y_0)=(x(t_0),y(t_0)))$处的切线方程与法线方程为：

$\frac{x-x_0}{x'(t_0)}=\frac{y-y_0}{y'(t_0)}\quad\quad \frac{x-x_0}{-y'(t_0)}=\frac{y-y_0}{x'(t_0)}$