信号 第二章:LTI系统的时域分析
2.1 CT LTI系统的时域分析
任意一个CT信号$x(t)$都可表示为加权、延迟单位冲激信号$\delta(t)$的叠加:
描述CT LTI系统的数学模型是线性常系数微分方程:
全响应$y(t)=$零输入响应$y_{zi}(t)+$零状态响应$y_{zs}(t)$=齐次解$y_h(t)$+特解$y_p(t)$
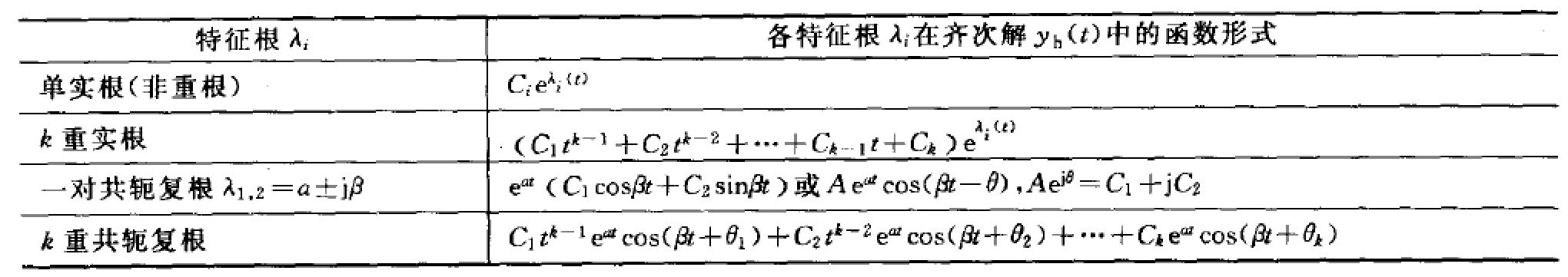
常见的齐次解形式:
单实根:$C_1e^{\lambda_1t}+C_2e^{\lambda_2t}…$
2重实根:$(C_1t+C_2)e^{\lambda t}$
一对共轭复根:$e^{\alpha t}(C_1\cos\beta t+C_2\sin\beta t)$

常见的特解形式:
$E$(常数):$C$
$t$:所有特征根都不等于0时:$C_1t+C_2$;有r重等于0的特征根时:$t^r(C_1t+C_2)$
$t^2$:所有特征根都不等于0时:$C_1t^2+C_2t+C_3$;有r重等于0的特征根时:$t^r(C_1t^2+C_2t+C_3)$
$e^{at}$:a不等于特征根时:$Ce^{at}$;a等于单根:$(C_1t+C_2)e^{at}$;a等于2重根:$(C_1t^2+C_2t+C_3)e^{at}$
$\cos\beta t$或$\sin\beta t$:$C_1\cos\beta t+C_2\sin \beta t$
求解全响应可用卷积积分法:
其中$h(t)$称为系统的单位冲激响应,可以表征系统时域特性。

单位冲激响应:LTI系统中,初始状态为0(零状态)时,输入为$\delta(t)$引起的响应;
单位阶跃响应:LTI系统中,初始状态为0(零状态)时,输入为$u(t)$引起的响应;
两者关系:
卷积:
①. 性质:
交换律、分配律、结合律
微分:
积分:
②. 与$\delta(t)$和$u(t)$的卷积:
③. 时移信号的卷积:
2.2 DT LTI系统的时域分析
任意一个CT信号$x[n]$都可表示为加权、延迟单位样值序列$\delta[n]$的叠加:
描述DT LTI系统的数学模型是线性常系数差分方程:
全响应$y[n]=$零输入响应$y_{zi}[n]+$零状态响应$y_{zs}[n]=$齐次解$y_h[n]$+特解$y_p[n]$
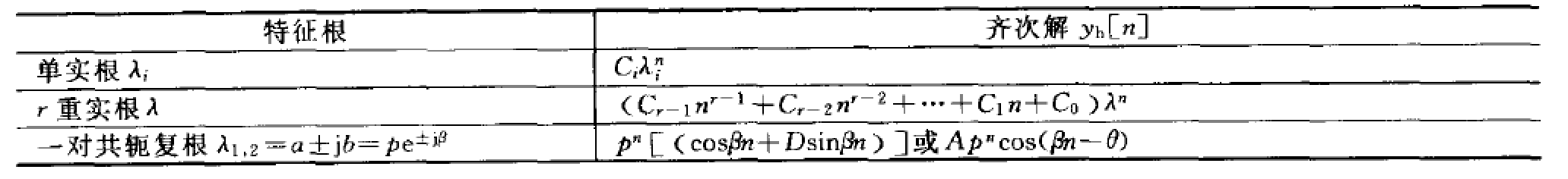
常见的齐次解形式:
单实根: $C_1\lambda_1^n+C_2\lambda_2^n…$
$2$重实根: $(C_1n+C_0)\lambda^n$
一对共轭复根$\lambda_{1,2}=a\pm jb=pe^{\pm j\beta}$: $p^n[(C\cos\beta n+D\sin \beta n)]$

常见的特解形式:
$n$: 所有特征根都不等于1,$D_1n+D_0$;$r$重特征根等于1:$n^r(D_1n+D_0)$
$a^n$: $a$不等于特征根,$Da^n$;$a$是$1$重特征根,$(D_1n+D_0)a^n$;$a$是$2$重特征根,$(D_2r^2+D_1r+D_0)a^n$
$\cos \beta n$或$\sin \beta n$:$P\cos \beta n+Q\sin\beta n$
求解全响应可用卷积和法:
其中$h(t)$称为系统的单位样值响应序列。

单位序列响应:LTI离散系统的激励是$\delta[n]$时,系统的零状态响应;
单位阶跃响应:LTI离散系统的激励是$u[n]$时,系统的零状态响应;
两者关系:
卷积和:
①. 性质:
交换律、结合律、分配律
②. 与$\delta[n]$和$u[n]$的卷积:
2.3 零输入、零状态响应
零输入响应$y_{zi}(t)$:不考虑外加输入信号的作用,仅由系统的起始状态所产生的响应;
零状态响应$y_{zs}(t)$:不考虑系统起始状态的作用,即起始状态等于零,仅由系统的外加激励信号所产的响应。(通过冲激函数)
冲激函数匹配法(常用来求解0时刻有输入突变的零状态响应参数):
①. 将输入$f(x)$代入微分方程,通过等号右端$\delta(t)$及其各阶导数,判断左端$y(t)$的最高阶数[对于二阶系统是$y’’(t)$]所含$\delta(t)$导数的最高阶次[例如为$\delta’’(t)$]
②. 令$y’’(t)=a\delta’’(t)+b\delta’(t)+c\delta(t)+r_0(t)$,对$y’’(t)$进行积分$(-\infty,t)$可求得$y’(t),y(t)$
③. 将$y’’(t),y’(t),y(t)$代入微分方程,根据$\delta(t)$及其各阶导数的系数相等来求出$y’’(t)$中的各待定系数
④. 分别对$y’(t),y’’(t)$等号两端从$0_-$到$0_+$进行积分,求得$y(0_+)$和$y(0_-)$
仅考虑特征根无重根的情况,系统响应的表示式为:
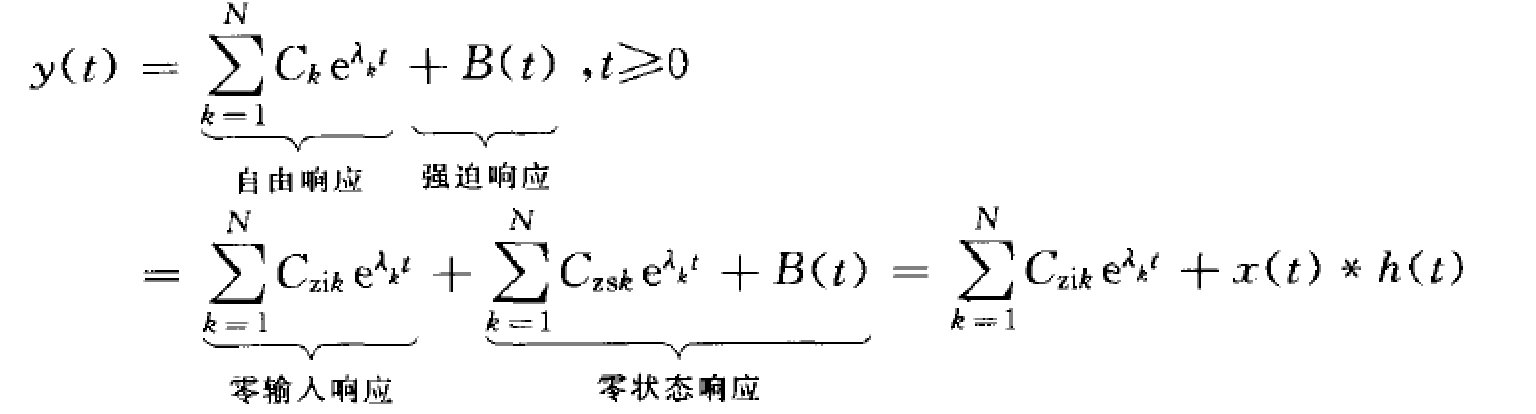
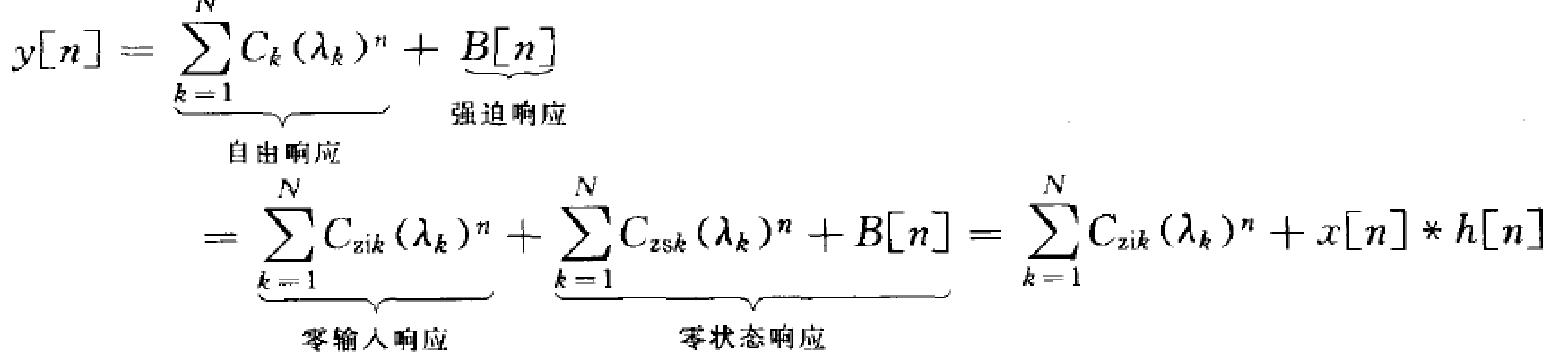
2.4 LTI系统的基本性质
①. 因果系统:
$CT: h(t)=0,t<0$
$DT: h[n]=0,n<0$
②. 稳定系统:
$CT: \int_{-\infty}^{\infty}|h(\tau)|d\tau<\infty$,绝对可积
$DT:\sum_{k=-\infty}^{\infty}|h[k]|<\infty$,绝对可和
③. 可逆系统:
$CT: h(t)\star h_1(t)=\delta(t)$
$DT: h[n]\star h_1[n]=\delta[n]$
$h_1(t),h_1[n]$分别为$h(t),h[n]$的逆系统
2.5 微分、差分方程表征的系统框图表示
微分方程表征CT LTI系统的框图
CT LTI系统的三个基本运算器是乘法器、加法器、积分器。
常系数线性微分方程:

差分方程表征DT LTI系统的框图
DT LTI系统的三个基本运算器是乘法器、加法器、单位延迟器。
线性常系数差分方程:

知识点补充
①. 因果LTI系统的逆系统不一定因果。比如$h[n]=\delta[n-k]$,逆系统为$g[n]=\delta[n+k]$
②. 若一个离散时间LTI系统的单位样值响应$h[n]$是有限的,则系统不一定是稳定的。例如:$h[n]=u[n]$,则$|h[n]|=1$,但$\sum_{n=-\infty}^{\infty}|h[n]|\to \infty$,系统不稳定。
③. 若$n<N_1,x[n]=0$和$n<N_2,h[n]=0$,那么$n<N_1+N_2$时$x[n]\star h[n]=0$;
同样,若$t>T_1,x(t)=0,t>T_2,h(t)=0$,则$t>T_1+T_2,x(t)\star h(t)=0$
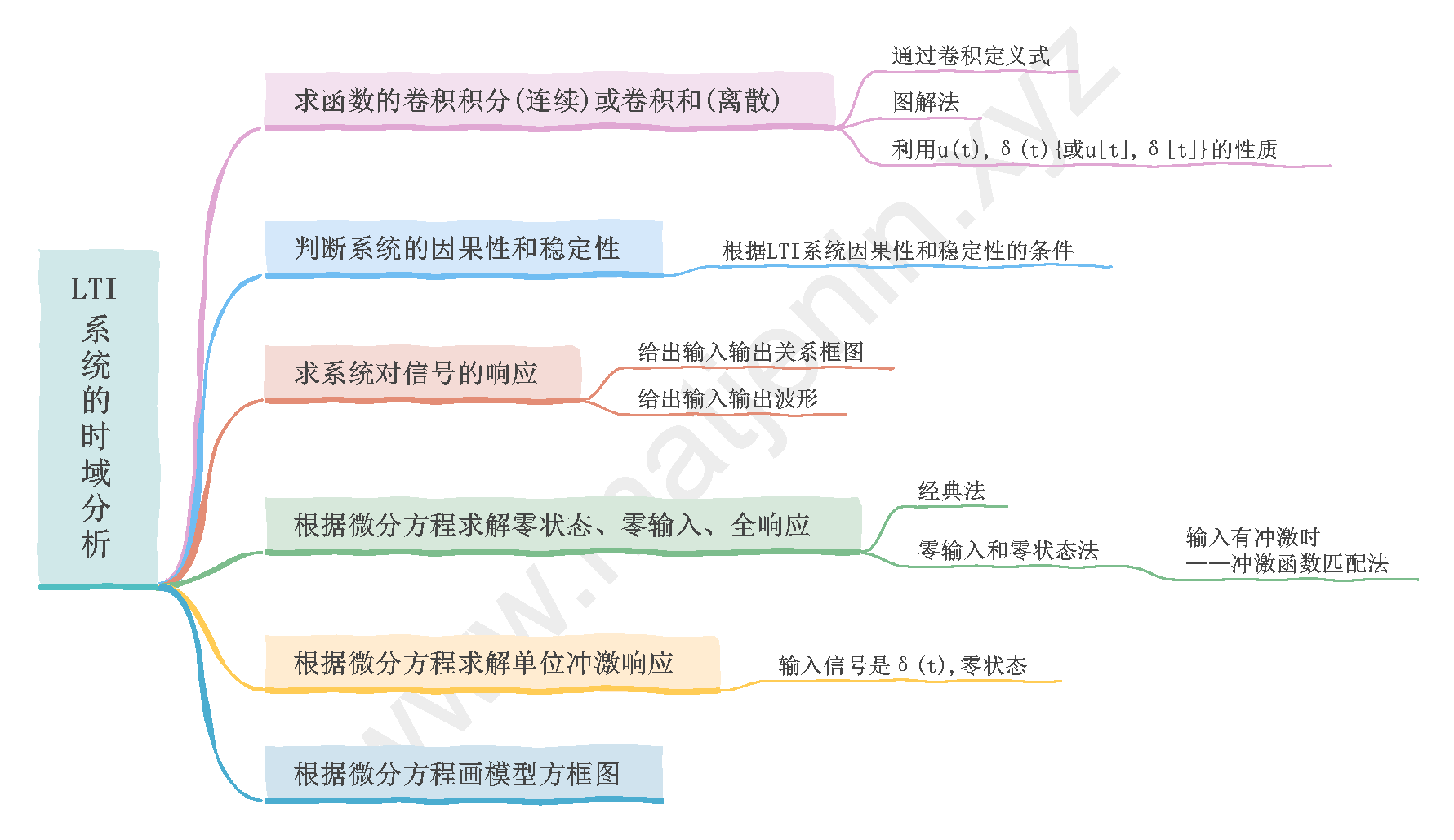
题型总结(强化)