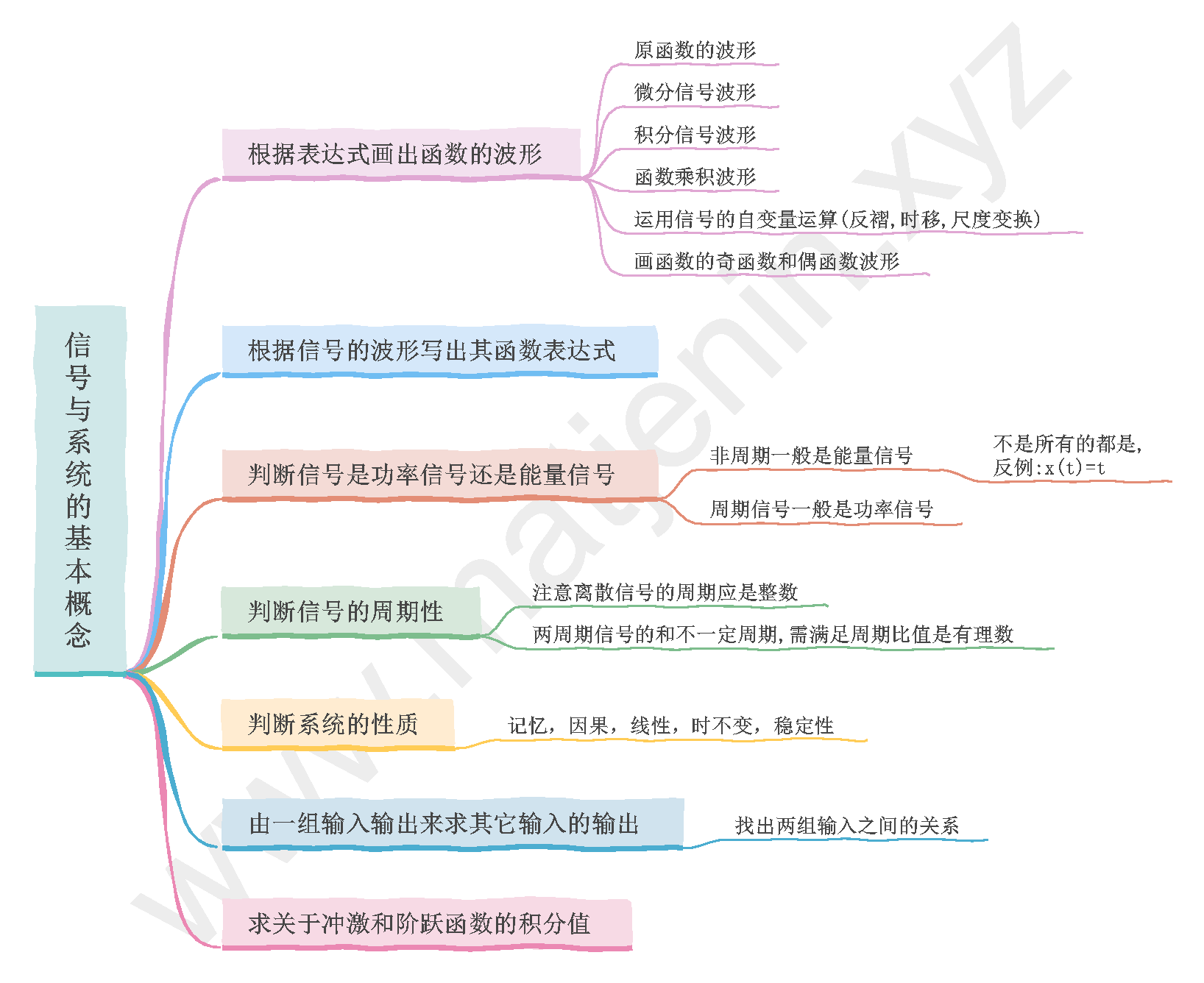
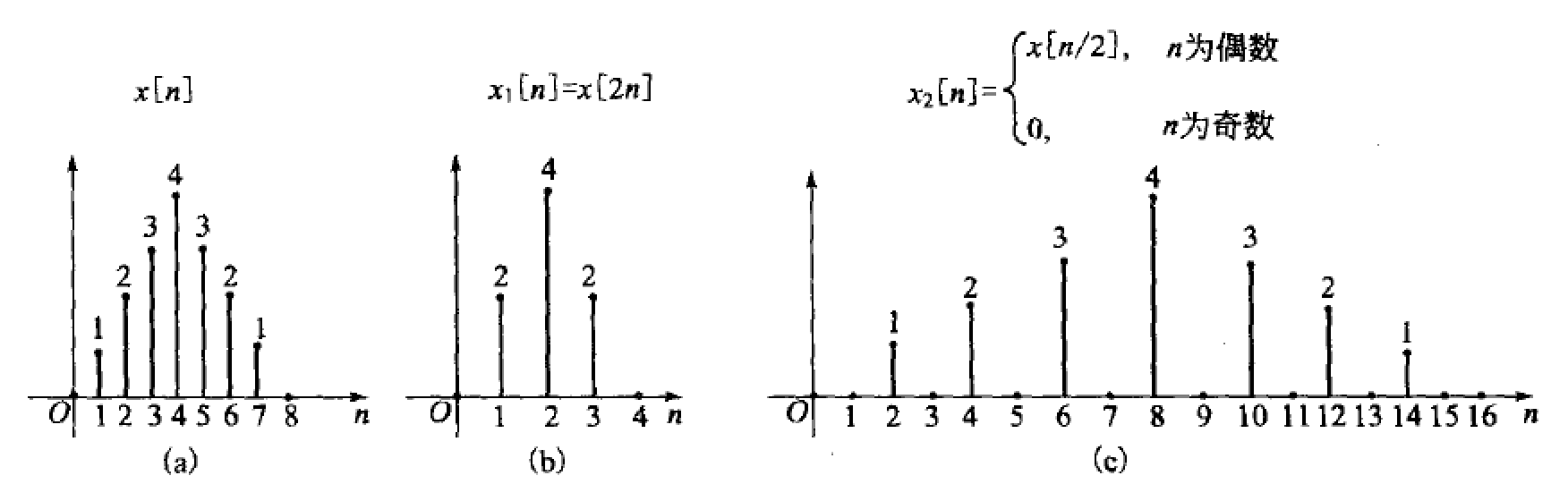信号 第一章：信号与系统的基本概念

1.1 CT与DT的基本信号

（CT：连续时间；DT：离散时间）

1.1.1 信号的分类

周期信号：

$$CT: x(t)=x(t+mT),m=0,\pm1,\pm2,...（最小正值T-基波周期）\\ DT: x[n]=x[n+mN],m=0,\pm1,\pm2,...（最小正整数N-基波周期）$$

能量信号，功率信号（无穷区间内）：

$$\begin{aligned} CT:E_{\infty}&=\lim_{T→\infty}\int_{-T}^T|x(t)|^2dt=\int_{-\infty}^{\infty}|x(t)|^2dt\\ P_{\infty}&=\lim_{T→\infty}\frac1{2T}\int_{-T}^T[x(t)]^2dt\\ DT:E_{\infty}&=\lim_{N→\infty}\sum_{n=-N}^N|x(n)|^2=\sum_{n=-\infty}^{\infty}|x[n]|^2\\ P_\infty&=\lim_{N→\infty}\frac1{2N+1}\sum_{n=-N}^N|x[n]|^2 \end{aligned}$$

功率有限，能量有限的信号是能量（有限）信号，能量无限的是功率（有限）信号；

一般来说，非周期信号是能量信号，周期信号是功率信号。

奇偶信号：

奇信号：$x(t)=-x(-t)$；偶信号：$x(t)=x(-t)$

任意一个信号都可写成：

$$x(t)=x_e(t)+x_o(t)$$

式中，偶分量$x_e(t)=\frac12[x(t)+x(-t)]$，奇分量$x_o(t)=\frac12[x(t)-x(-t)]$

1.1.2 基本的CT信号

复指数信号：$x(t)=ce^{st}$，$c$可为复数，$s=σ+j\omega_0$

奇异信号：本身或其导数和积分有不连续的信号

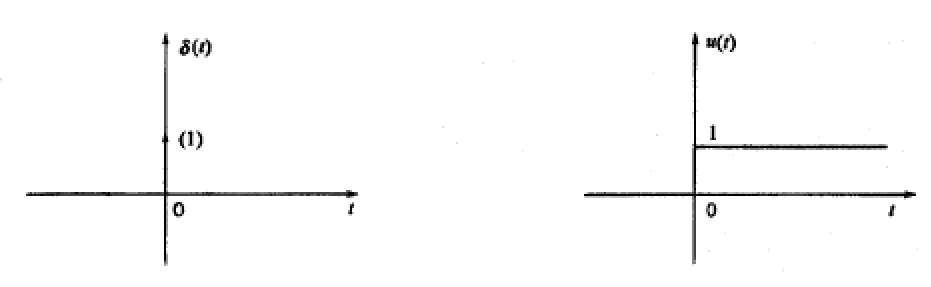
①. $\delta(t)$：单位冲激信号，$\delta(t)=0\ (t\ne 0),\ \ \int_{-\infty}^{\infty}\delta(t)dt=1$

②. $u(t)$：单位阶跃信号，$u(t)=\begin{cases}1,&t>0\\0,&t<0 \end{cases}(t=0不确定)$

③. $\delta’(t)$：冲激偶信号，$\delta’(t)=\frac{d\delta(t)}{dt}$

④. 斜波信号：$r(t)=\begin{cases}t,&t>0\\0,&t<0 \end{cases}$

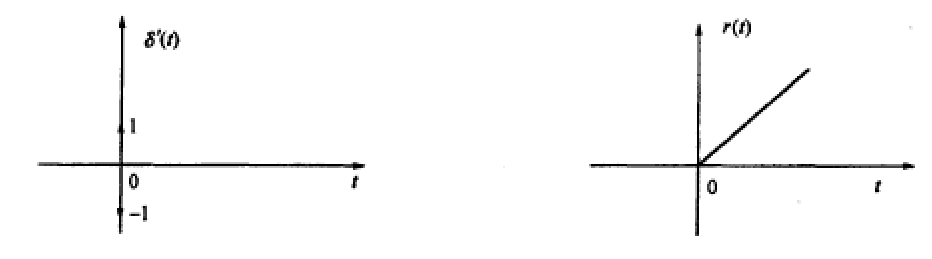
奇异信号的性质：

$$\begin{aligned} x(t)\delta(t)=x(0)\delta(t)&\quad\quad x(t)\delta'(t)=x(0)\delta'(t)-x'(0)\delta(t)\\ x(t)\delta(t-t_0)=x(t_0)\delta(t-t_0)&\quad\quad x(t)\delta'(t-t_0)=x(t_0)\delta'(t-t_0)-x'(t_0)\delta(t-t_0)\\ \int_{-\infty}^{\infty}x(t)\delta(t)dt=x(0)&\quad\quad \int_{-\infty}^{\infty}x(t)\delta(t-t_0)dt=x(t_0)\\ \int_{-\infty}^{\infty}x(t)\delta'(t)dt=-x'(0)&\quad\quad \int_{-\infty}^{\infty}x(t)\delta'(t-t_0)dt=-x'(t_0)\\ \int_{-\infty}^{\infty}x(t)\delta^{(n)}(t)dt=(-1)^nx^{(n)}(0)&\quad\quad \int_{-\infty}^{\infty}x(t)\delta^{(n)}(t-t_0)dt=(-1)^nx^{(n)}(t_0)\\ \int_{-\infty}^{\infty}\delta'(t)dt=0&\quad\quad \delta(t)=\delta(-t)\\ \delta(at+b)=\frac1{|a|}\delta(t+\frac ba)&\\ \delta(t)=\frac{du(t)}{dt}&\quad\quad u(t)=\int_{-\infty}^t\delta(τ)dτ\\ u(t)=\frac{dr(t)}{dt}&\quad\quad\int_{-\infty}^tu(τ)dτ=r(t)\\ \end{aligned}$$

$\delta(t)=u(t)-u(t-1)$错误，在DT信号中才满足$\delta[n]=u[n]-u[n-1]$。

常用其它CT信号：

①. 抽样信号$Sa(t)=\frac{\sin(t)}{t}$，性质如下：

$$\lim_{t\to 0}Sa(t)=1\quad\quad \lim_{t\to \pm\infty}Sa(t)=0\\ Sa(t)=Sa(-t)\quad\quad \int_{-\infty}^{\infty}Sa(t)dt=\pi\\ Sa(t)=0,t=k\pi(k=\pm1,\pm2,\pm3,...)$$

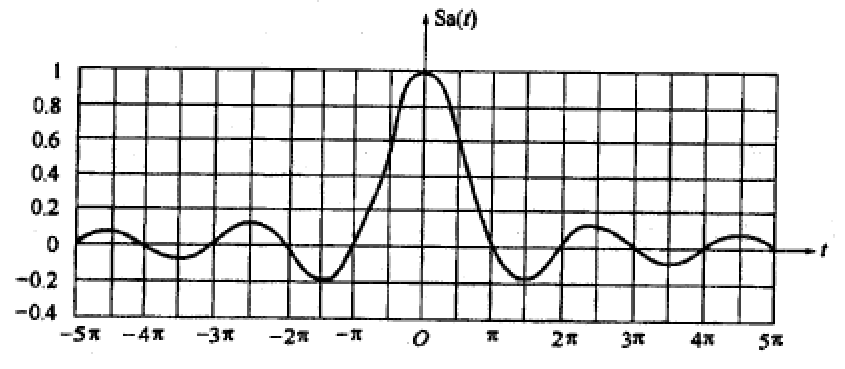
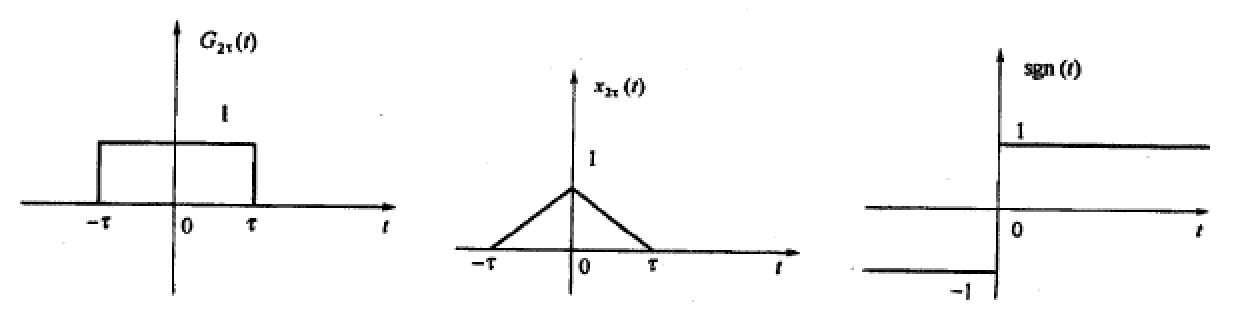
②. 方波脉冲信号：$G_{2τ}(t)=\begin{cases}1,&|t|<τ\\0,&|t|>τ \end{cases}$

③. 三角脉冲信号：$x_{2τ}(t)=\begin{cases}1-\frac{|t|}{τ},&|t|<τ\\0,&其它 \end{cases}$

④. 符号函数：$sgn(t)=\begin{cases}-1,&t<0\\1,&t>0 \end{cases}=2u(t)-1=u(t)-u(-t)$

1.1.3 基本的DT序列

单位样值序列：$\delta[n]=\begin{cases}1,&n=0\\0,&其它 \end{cases}$，是可表示任意DT信号的基本信号

单位阶跃序列：$u[n]=\begin{cases}1,&n\ge 0\\0,&其它 \end{cases}$

斜波序列：$r[n]=\begin{cases}n,&n\ge 0\\0,&n<0 \end{cases}$

矩形序列：$G_N[n]=\begin{cases}1,&0\lt n\le N-1\\0,&其它\end{cases}$

相互关系：

$$\begin{align} \delta[n]=u[n]-u[n-1]&\quad\quad u[n]=\sum_{k=-\infty}^n\delta[k]\\ x[n]\delta[n]=x[0]\delta[n]&\quad\quad x[n]\delta[n-n_0]=x[n_0]\delta[n-n_0]\\ \end{align}$$ $$G_N[n]=u[n]-n[u-N]$$

离散复指数序列：$x[n]=ce^{\beta n}$

$x[n]=ce^{j\omega_0n}$是DT信号频域分析中的基本信号，不一定是n的周期信号，必须满足：$\frac{\omega_0}{2\pi}=\frac{m}{N}$为有理数。

如果$x[n]$是一个周期序列，基波周期为$N$（多个不同周期的信号相加时的周期为公们的公倍数），则它的基波频率为$\frac{2\pi}N=\frac{\omega_0}{m}$。

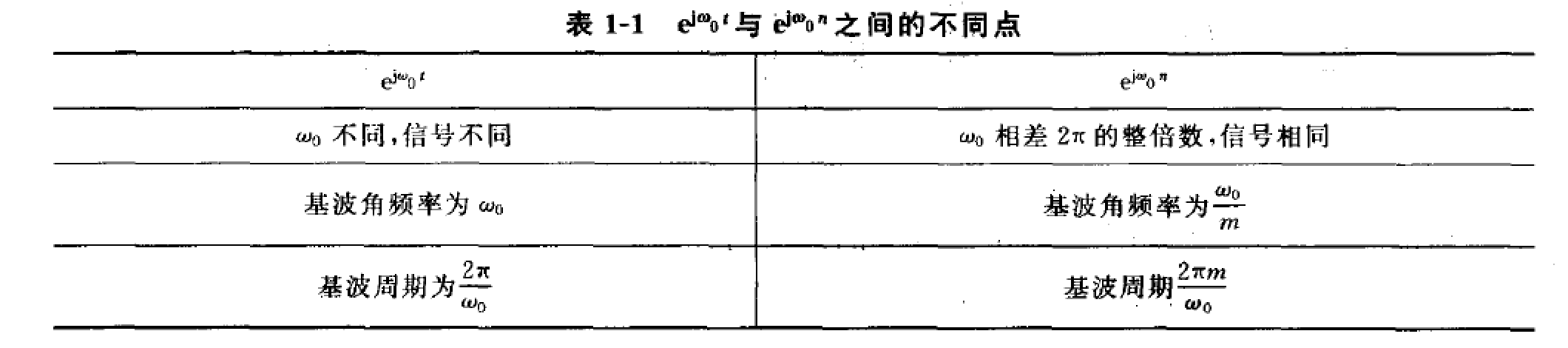
$e^{j\omega_0t}$与$e^{j\omega_0 n}$的重要区别，对于$e^{j\omega_0t}$，不同的$\omega_0$即表示不同的连续信号，$\omega_0$越大，信号振荡的速率越高；而$e^{j\omega_0n}$不同，它具有对$\omega_0$的周期性。

1.2 信号的运算与自变量变换

基本运算：相加，相乘，微分，差分$(▽x[n]=x[n]-x[n-1])$，积分，累加

自变量变换：

①. 反褶：$x(t)\to x(-t)$，以纵坐标为轴折叠

②. 时移：$x(t)\to x(t-t_0)$

③. 尺度变换：$x(at),x(at+\beta)$

对于离散时间序列的尺度变换规则：

1、抽取：$x_1[n]=x[N·n],(N为正整数)$，表示以$N-1$个点为间隔选取相应的序列点并重新依次排序。

2、内插：$x_1[n]=\begin{cases}x[n/N],&{n为N的整数倍}\\0,&{其他N}\end{cases}$，表示在$x[n]$序列相邻两序号之间插入$N-1$个零值后所构成的序列。

1.3 LTI系统的基本性质

1.3.1 LTI系统的数学模型

CT：N阶线性常系数微分方程：

$$\sum_{k=0}^Na_k\frac{d^ky(t)}{dt^k}=\sum_{k=0}^Mb_k\frac{d^kx(t)}{dt^k}$$

DT：N阶线性常系数微分方程：

$$\sum_{k=0}^Na_ky[n-k]=\sum_{k=0}^Mb_kx[n-k]$$

1.3.2 LTI系统的性质

①. 线性：齐次性和叠加性

$$ax_1(t)+bx_2(t)\to ay_1(t)+by_2(t)\\ ax_1[n]+bx_2[n]\to ay_1[n]+by_2[n]$$

②. 时不变性：

$$x(t)\to y(t),\quad\quad 则x(t-t_0)\to y(t-t_0)\\ x[n]\to y[n],\quad\quad 则x[n-n_0]\to y[n-n_0]$$

③. 记忆性：无记忆性系统的输出只与当前输入时刻有关。

④. 因果性：系统的输出只与现在和过去的输入有关。（无记忆性必因果）

⑤. 可逆性：输出和输入可逆，输入输出”一一对应“。

⑥. 稳定性：依据在有界的输入下能否产生有界的输出进行判定。

易错点

判断系统的性质

①. $y(t)=\frac{dx}{dt}$：因为$\frac{dx}{dt}=\lim_{△t\to 0}\frac{x(t+△t)-x(t)}{△t}$，可以看出输出和之前的时间的输入有关，故该系统是有记忆的、因果的。容易判断该系统也是线性、时不变、不稳定的。

②. $y(t)=\sin(4t)x(t)$：容易判断该系统是无记忆、因果、稳定的；因为$\sin(4t)[ax_1(t)+bx_2(t)]=ay_1(t)+by_2(t)$，故是线性的；因为$y(t-t_0)=\sin[4(t-t_0)]x(t-t_0)\ne \sin(4t)x(t-t_0)$，故是时变的。

③. $y[n]=x[4n]$：$n$时刻的输出和$4n$时刻的输入有关，故该系统是有记忆、非因果的；容易判断该系统是线性的、稳定的；$y[n-n_0]=x[4(n-n_0)]\ne x[4n-n_0]$，故是时变的。

⑥. $y(t)=\begin{cases}0,&{t<0}\\x(t)+x(t-50),&t\ge 0 \end{cases}$，容易判定线性，有线性，记忆，因果，若$x(t)$有界则稳定。现讨论时变：

$$\begin{aligned} x(t-t_0)&\Leftrightarrow \begin{cases}0,&{t<0}\\x(t-t_0)+x(t-50-t_0),&t\ge 0 \end{cases}\\ &\ne y(t-t_0)=\begin{cases}0,&{t<t_0}\\x(t-t_0)+x(t-50-t_0),&t\ge t_0 \end{cases} \end{aligned}$$

故是时变的。

求含冲激函数的积分值

$$\int_{-\infty}^{\infty}\delta(2t-1)x(t)dt=\frac12\int_{-\infty}^{\infty}\delta(t-\frac12)x(t)dt=\frac12x(\frac12)$$

零碎的知识点

①. 不是所有非周期信号都是能量信号，比如$y(t)=t$

②. 两个周期信号之和不一定是周期信号，需满足周期之比是有理数

题型总结