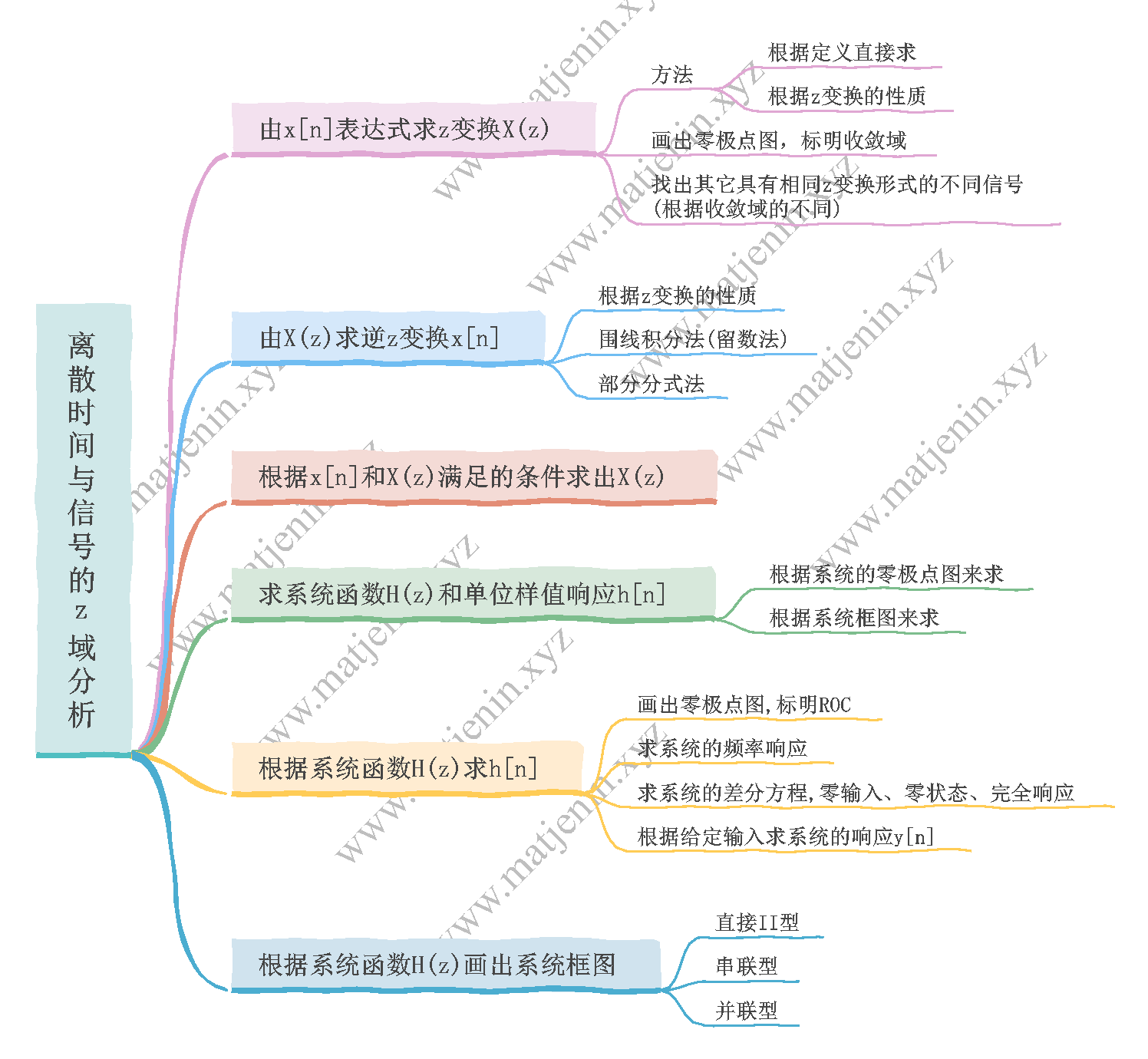
信号 第七章:离散时间信号与系统的Z域分析
7.1 z变换定义、零极点图及收敛域
7.1.1 z变换定义
其中$z=re^{j\omega}$,为一复变量。
7.1.2 零、极点图
一般来说,信号$x[n]$的$z$变化可表示成有理函数形式:
$N(z)$的根$z_i$称为零点,$D(z)$的根$p_i$称为极点。
7.1.3 收敛域
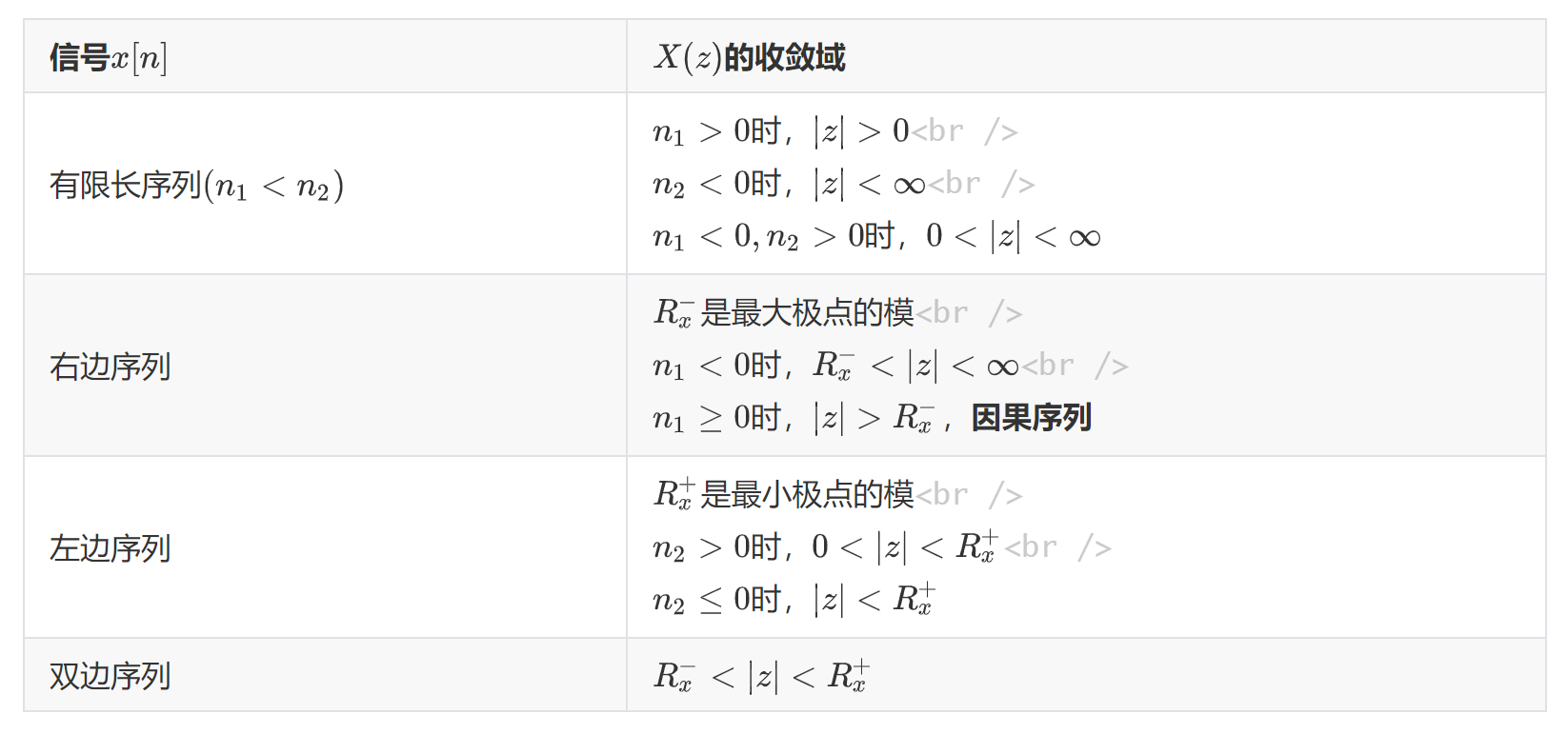
7.2 z变换性质


终值定理的条件:极点均落于单位圆内(单位圆上最多在$z=1$处有一阶极点)。
7.3 常见信号的z变换
有限长信号:
因果信号:
7.4 z逆变换
定义:
其中$c$是$X(z)$的收敛域内包围原点的逆时针方向的闭合曲线。
求解方法:
①. 围线积分法(留数法):
需要从$n$的取值讨论$z=0$是不是极点的情况。
若$X(z)z^{n-1}$在$z=z_m$处有一阶极点,则有:
若$X(z)z^{n-1}$在$z=z_m$处有$k$阶极点,则有:
②. 幂级数展开法:
对于有理$z$变换而言,幂级数展开可采用长除法得到:
- 如果$X(z)$的收敛域是$|z|>R_x^-$,则$x[n]$必然是因果序列,此时$N(z)$和$D(z)$按$z$的降幂(即$z^{-1}$的升幂)次序进行排列;
- 如果$X(z)$的收敛域是$|z|<R_x^-$,则$x[n]$必然是左边序列,此时$N(z)$和$D(z)$按$z$的升幂(即$z^{-1}$的降幂)次序进行排列;
③. 部分分式展开法:
1、若$n\ge m$,且所有极点$p_k$为单极点,则
其中
2、若$n\lt m$,则
如果$X(z)$具有多重极点(设$p_i$为$r$重极点),则$X(z)/z$的展开式为:
其中:
7.5 系统函数
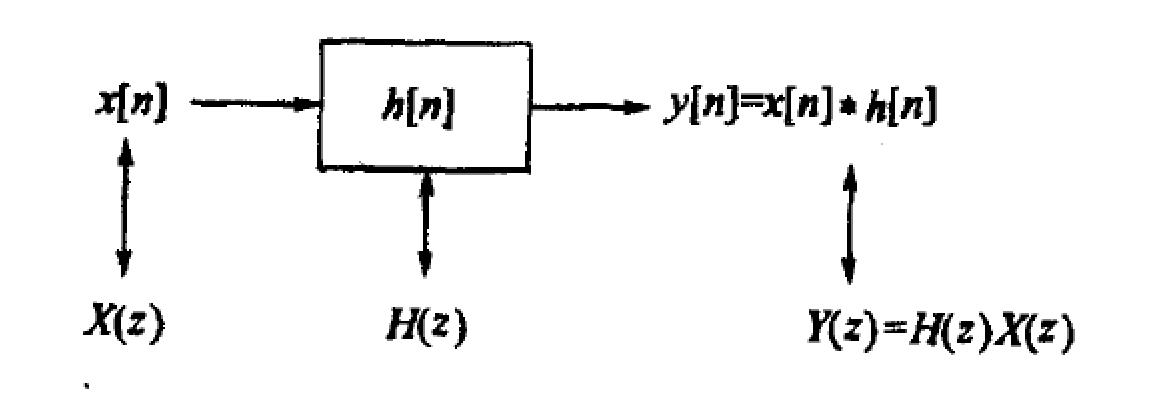
系统函数:
LTI系统的因果性和稳定性:
①. 因果系统:当且仅当一个离散LTI系统的系统函数$H(z)$的$ROC$在某一个圆的外部,且包含无穷远点$\infty$,该系统因果;
②. 稳定系统:当且仅当一个离散LTI系统的系统函数$H(z)$的$ROC$包含单位圆,该系统稳定。
7.6 离散LTI系统的z域分析
利用单边$z$变换来分析离散LTI系统非常有效,因为它包含了系统的初始条件,从而可以方便地求得零输入、零状态响应。
①. 若给定差分方程,则对两边进行单边$z$变换(利用移位性质并代入初始条件)得到$Y(z)$,并将$Y(z)$分解成只与初始条件有关和只与输入信号有关的两部分,再做逆变换,即可对应得到零输入和零状态响应;
②. 若给定系统函数$H(z)$,则首先由$Y(z)=H(z)X(z)$做逆变换可求得零状态响应;再求出差分方程,利用移位性质并代入初始条件进行变换(此时令输入为0),最后做逆变换求出零输入响应。
7.7 离散LTI系统的频率响应
单位圆上计算$z$变换即得离散LTI系统的频率响应:
频率响应的几何确定法:
其中$A_r$表示$z$平面上零点至单位圆上某点的长度。

有时会利用到极坐标距离公式:$|AB|=\sqrt{ρ_1^2+ρ_2^2-2ρ_1^2ρ_2^2\cos(\theta_1-\theta_2)}$
7.8 z域系统框图表示
一个$N$阶的离散系统的差分方程可表示为:
上式所对应的系统函数为:
可描述成框图:
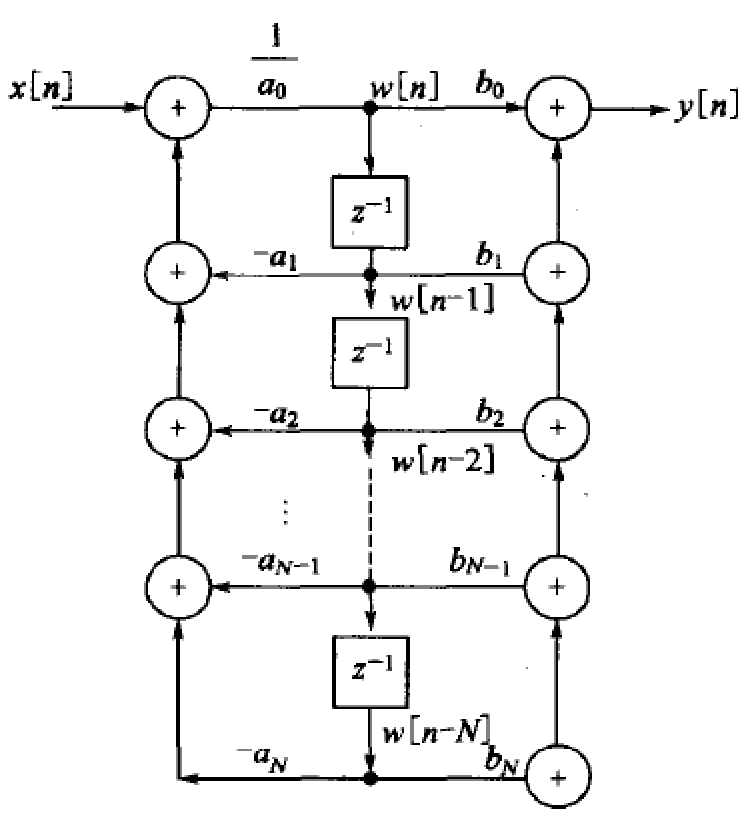
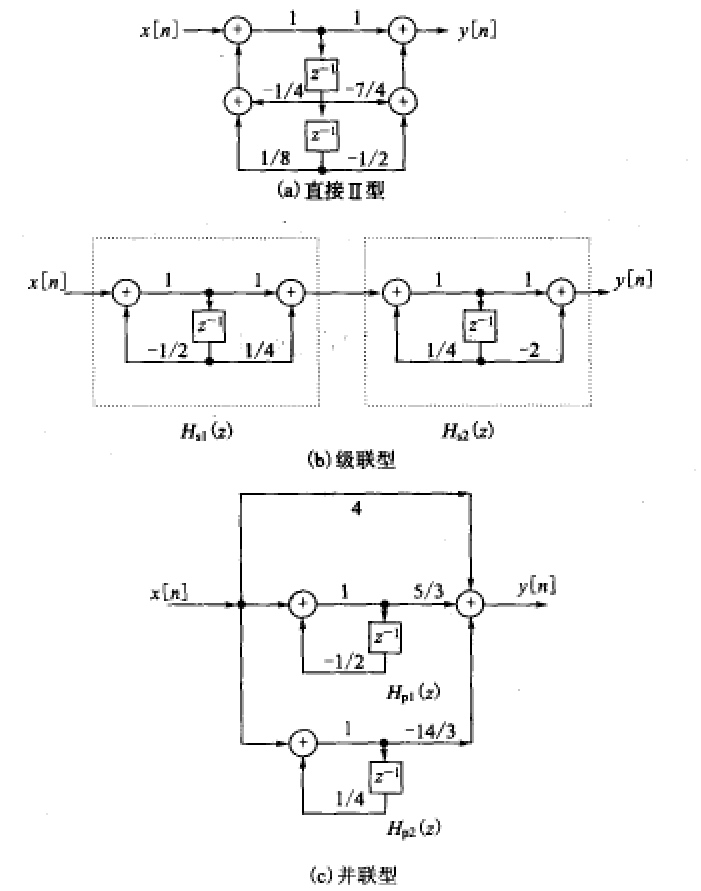
上式的直接型、级联型、并联型框图如下所示:
补充知识点
①. 对于一因果离散LTI系统,$\sum_{i=0}^n x[i]=x[n]\star u[n]$
题型总结(强化)