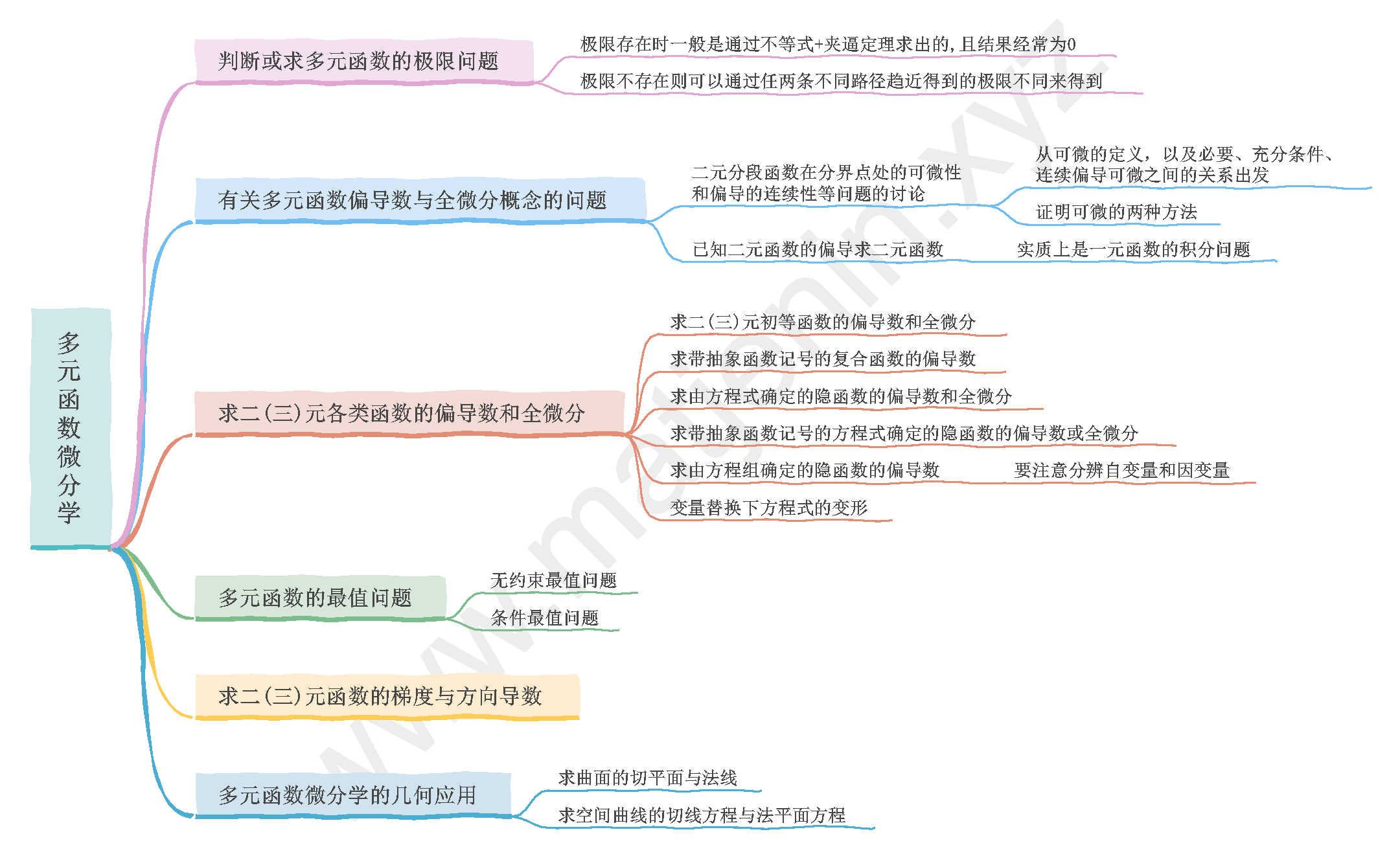
数一高数 第八章：多元函数微分学

第一节 多元函数的基本概念

一、二元函数

$$z=f(x,y)$$

在几何上表示一张空间曲面。

二、二元函数的极限

$$\lim_{(x,y)→(x_0,y_0)}f(x,y)=A$$

前提是以任意方式趋近。

一元函数极限的性质仍成立的有：局部有界性、保号性、极限与无穷小的关系、夹逼性。（不包括洛必达）

掌握：

1、求解简单的多元函数极限：常用夹逼（必要时加绝对值）；

2、说明多元函数极限不存在的方法：找两个不同的路径。

三、多元函数的连续性、

1. 连续的概念

$$\lim_{(x,y)→(x_0,y_0)}f(x,y)=f(x_0,y_0)$$

2. 连续函数的性质

• 多元连续函数的和、差、积、商（分母不为0）仍连续；
• 多元连续函数的复合函数也连续；
• 多元初等函数在其定义区域内连续；
• 最大值定理： 有界闭区域$D$上的连续函数在区域$D$上必能取得最大值与最小值；
• 介值定理： 有界闭区域$D$上的连续函数在区域$D$上必能取得最大值与最小值之间的任意值。

掌握：利用定义判断多元函数的连续性。

四、偏导数

1. 偏导数的定义

$$f'_x(x_0,y_0)=\lim_{△x→0}\frac{f(x_0+△x,y_0)-f(x_0,y_0)}{△x}=\frac d{dx}f(x,y_0)|_{x=x_0}$$ $$f'_y(x_0,y_0)=\lim_{△y→0}\frac{f(x_0,y_0+△y)-f(x_0,y_0)}{△y}=\frac d{dy}f(x_0,y)|_{y=y_0}$$

2. 二元函数偏导数的几何意义

$f’_x(x_0,y_0)$表示交线$\begin{cases}z=f(x,y_0)\\y=y_0\end{cases}$在点$(x_0,y_0,f(x_0,y_0))$处的切线对$x$轴的斜率。

3. 高阶偏导数

$$\frac\partial{\partial x}(\frac{\partial z}{\partial x})=\frac{\partial^2 z}{\partial x^2}=f''_{xx}\quad \quad\frac\partial{\partial y}(\frac{\partial z}{\partial x})=\frac{\partial^2 z}{\partial x\partial y}=f''_{xy}\\ \frac\partial{\partial x}(\frac{\partial z}{\partial y})=\frac{\partial^2 z}{\partial y\partial x}=f''_{yx}\quad \quad \frac\partial{\partial y}(\frac{\partial z}{\partial y})=\frac{\partial^2 z}{\partial y^2}=f''_{yy}$$

定理：$\frac{\partial^2 z}{\partial x\partial y}$和$\frac{\partial^2 z}{\partial y\partial x}$在区域$D$内连续，则在该区域内：

$$\frac{\partial^2 z}{\partial x\partial y}=\frac{\partial^2 z}{\partial y\partial x}$$

五、全微分

定义：若：

$$\begin{aligned}△z &=f(x_0+△x,y_0+△y)-f(x_0,y_0)\\ &=A△x+B△y+o(ρ) \end{aligned}$$

其中$ρ=\sqrt{(△x)^2+(△y)^2}$，则称函数$z=f(x,y)$在点$(x,y)$处可微， 全微分记为：

$$dz=A△x+B△y$$

可微的必要条件：如果$z=f(x,y)$在点$(x,y)$处可微，则在点$(x,y)$处$\frac{\partial z}{\partial x}$,$\frac{\partial z}{\partial y}$必定存在，且：

$$dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy$$

可微的充分条件：如果$z=f(x,y)$的偏导数$\frac{\partial z}{\partial x}$,$\frac{\partial z}{\partial y}$在点$(x,y)$处连续，则函数$z=f(x,y)$可微。

用定义判断可微：

①. $f’_x(x_0,y_0)$与$f’_y(x_0,y_0)$是否都存在？

②.

$$\lim_{△x→0\\△y→0}\frac{[f(x_0+△x,y_0+△y)-f(x_0,y_0)]-[f'_x(x_0,y_0)△x+f'_y(x_0,y_0)△y]}{\sqrt{(△x)^2+(△y)^2}}$$

是否为0？

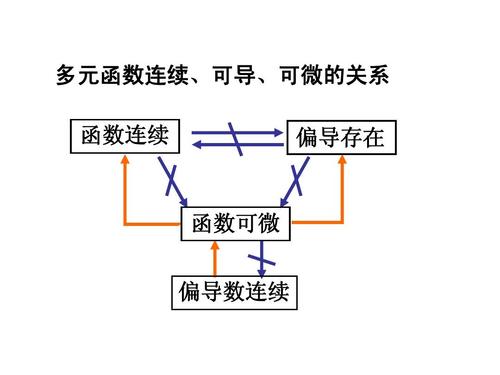
掌握：连续、可偏导、可微的概念及其之间的关系。

第二节 多元函数的微分法

一、复合函数的微分法

定理：设$u=u(x,y)$，$v=v(x,y)$在点$(x,y)$处有对$x$及对$y$的偏导数，函数$z=f(u,v)$在对应点$(u,v)$处有连续偏导数，则$z=f[u(x,y),v(x,y)]$在点$(x,y)$处的两个偏导数存在，且有：

$$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial x}\quad \quad \frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial y}$$

全微分形式的不变性：

设函数$z=f(u,v)$，$u=u(x,y)$及$v=v(x,y)$都有连续的一阶偏导数，则复合函数$z=f[u(x,y),v(x,y)]$的全微分：

$$dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy=\frac{\partial z}{\partial u}du+\frac{\partial z}{\partial v}dv$$

二、隐函数微分法

①. 由方程$F(x,y)=0$确定的隐函数$y=y(x)$

若函数$F(x,y)$在点$P(x_0,y_0)$的某一邻域内有连续偏导数，且$F(x_0,y_0)=0$，$F’(x_0,y_0)\ne 0$，则方程$F(x,y)=0$在点$(x_0,y_0)$的某邻域可唯一地确定一个有连续导数的函数$f(x)$，并有：

$$y'=-\frac{F'_x}{F'_y}$$

②. 由方程$F(x,y,z)=0$确定的隐函数$z=z(x,y)$

若函数$F(x,y,z)$在点$P(x_0,y_0,z_0)$的某一邻域内有连续偏导数，且$F(x_0,y_0,z_0)=0$，$F’_z(x_0,y_0,z_0)\ne 0$，则方程$F(x,y,z)=0$在点$(x_0,y_0,z_0)$的某邻域可唯一地确定一个有连续偏导数的函数$z=z(x,y)$，并有：

$$\frac{\partial z}{\partial x}=-\frac{F'_x}{F'_z}\quad \quad \frac{\partial z}{\partial y}=-\frac{F'_y}{F'_z}$$

求法一：由$F(x,y,z(x,y))=0$分别对自变量$x,y$求偏导，应用复合函数求导法得：

$$F'_x+F'_z\frac{\partial z}{\partial x}=0,\quad\quad\quad F'_y+F'_z\frac{\partial z}{\partial y}=0$$

求法二：利用一阶全微分形式不变性，对方程$F(x,y,z)=0$两边求全微分：

$$dF(x,y,z)=0\to F'_xdx+F'_ydy+F'_zdz=0$$

③. 求由$F(x,y,z)=0$确定的隐函数$z=z(x,y)$二阶偏导数的方法：

• 在求完一阶的隐函数微分方程基础上再求一阶（有时比第二种简便）
• 先把$\frac{\partial z}{\partial x}$提出来，再对它求一阶导

④. 由方程组$\begin{cases}F_1(x,y,u,v)=0\\F_2(x,y,u,v)=0\end{cases}$确定的隐函数$u=u(x,y)$，$v=v(x,y)$

将每个方程分别求对$x,y$的偏导数，然后解方程组。

第三节 多元函数的极值与最值

一、无约束极值

极值的必要条件：设$z=f(x,y)$在点$(x_0,y_0)$存在偏导数，且$(x_0,y_0)$为$(x,y)$的极值点，则：

$$f'_x(x_0,y_0)=f'_y(x_0,y_0)=0$$

极值的充分条件：设$z=f(x,y)$在点$P_0(x_0,y_0)$的某邻域内有二阶连续导数，又$f’_x(x_0,y_0)=0$，$f’_y(x_0,y_0)=0$，记：

$$A=f''_{xx}(x_0,y_0)\quad B=f''_{xy}(x_0,y_0)\quad C=f''_{yy}(x_0,y_0)$$

则有下述结论：

①. 若$AC-B^2>0$，则$(x_0,y_0)$为极值点：

• $A<0$，则为极大值点；
• $A>0$，则为极小值点。

②. 若$AC-B^2<0$，则$(x_0,y_0)$不为极值点；

③. 若$AC-B^2=0$，则不确定，此时需用定义判定。

二元函数可能是极值点的点：驻点和偏导数不存在的点。

二、条件极值及拉格朗日乘数法

求$z=f(x,y)$在条件$\varphi(x,y)=0$下的条件极值：

①. 构造拉格朗日函数$F(x,y,λ)=f(x,y)+λ\varphi(x,y)$

②. 分别对$x,y,λ$求偏导，构造方程组：

$$\begin{cases} f'_x(x,y)+λ\varphi'_x(x,y)=0\\ f'_y(x,y)+λ\varphi'_y(x,y)=0\\ \varphi(x,y)=0 \end{cases}$$

可推广

强化：拉格朗日乘数法方程组四种解法：

①. 消去$\lambda$（需要讨论$\lambda$是否等于$0$）；②. 轮换对称性（容易漏条件，紧急情况用）；③. 齐次解$\lambda$（原理是欧拉方程）；④. 将条件代入到原式中。

三、最值

找最大最小值：找到所有可能的极值点和边界上的最大最小值，进行比较。

第四节 多元函数微分学的几何应用

一、空间曲面的切平面与法线

①. 用隐式方程表示的曲面

若空间曲面$S$的方程为$F(x,y,z)=0,M_0(x_0,y_0,z_0)$是$S$上的一点，则$S$在$M_0$点的切平面方程为：

$$\frac{\partial F(M_0)}{\partial x}(x-x_0)+\frac{\partial F(M_0)}{\partial y}(y-y_0)+\frac{\partial F(M_0)}{\partial z}(z-z_0)=0$$

曲线在该点的法线方程为

$$\frac{x-x_0}{\frac{\partial F(M_0)}{\partial x}}=\frac{y-y_0}{\frac{\partial F(M_0)}{\partial y}}=\frac{z-z_0}{\frac{\partial F(M_0)}{\partial z}}$$

②. 用显式方程表示的曲面

若空间曲面$S$的方程为$z=f(x,y),M_0(x_0,y_0,z_0)$是$S$上的一点，$z_0=f(x_0,y_0)$，则曲面$S$在$M_0$的切平面方程为：

$$z-z_0=f'_x(x_0,y_0)(x-x_0)+f'_y(x_0,y_0)(y-y_0)$$

曲线在该点的法线方程为：

$$\frac{x-x_0}{f'_x(x_0,y_0)}=\frac{y-y_0}{f'_y(x_0,y_0)}=\frac{z-z_0}{-1}$$

二、空间曲线的切线与法平面

①. 用参数方程表示的空间曲线

若空间曲线$\Gamma$的参数方程为$x=x(t),y=y(t),z=z(t)\ (\alpha\le t\le\beta)$，又$M_0(x_0,y_0,z_0)=(x(t_0),y(t_0),z(t_0))$是$\Gamma$上的一点，则$\Gamma$在点$M_0$的切线方程为：

$$\frac{x-x_0}{x'(t_0)}=\frac{y-y_0}{y'(t_0)}=\frac{z-z_0}{z'(t_0)}$$

法平面方程为：

$$x'(t_0)(x-x_0)+y'(t_0)(y-y_0)+z'(t_0)(z-z_0)=0$$

②. 作为两曲面交线的空间曲线

若空间曲线$\Gamma$的一般方程为$\begin{cases}F(x,y,z)=0\\G(x,y,z)=0 \end{cases}$，$M_0$是$\Gamma$上的一点，则$\Gamma$在点$M_0$的切线方程为：

$$\begin{cases} \frac{\partial F(M_0)}{\partial x}(x-x_0)+\frac{\partial F(M_0)}{\partial y}(y-y_0)+\frac{\partial F(M_0)}{\partial z}(z-z_0)=0\\ \frac{\partial G(M_0)}{\partial x}(x-x_0)+\frac{\partial G(M_0)}{\partial y}(y-y_0)+\frac{\partial G(M_0)}{\partial z}(z-z_0)=0 \end{cases}$$

技巧知识点

①. $\lim_{(x,y)\to(0,0)}\alpha=0$

$$\lim_{(x,y)\to (0,0)}\frac{f(x,y)-1}{x^2+y^2}=2\quad\quad\quad\Rightarrow \quad \quad\quad\quad f(0,0)=1\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad↓\\ \quad\quad\quad\quad\begin{aligned} &\quad\ {f(x,y)-f(0,0)}\\&=(2+\alpha){(x^2+y^2)}\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad&=o(ρ)\\&=0\cdot △x+0\cdot △y+o(ρ) \end{aligned}\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad↓\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad f'_x(0,0)=f'_y(0,0)=0$$

②. 偏导也是二元函数，所以偏导连续也需要保证以任意方向趋近都连续。即$\lim_{(x,y)\to (0,0)}f’_x(x,y)=f’_x(0,0)$而不是$\lim_{x\to 0}f’_x(x,0)=f’_x(0,0)$（660 237题）

③. 在闭区域上函数有唯一极大值点，则$f(x,y)$在该点不一定是最大值点（一元成立，二元不成立）

④.

题型总结（强化）