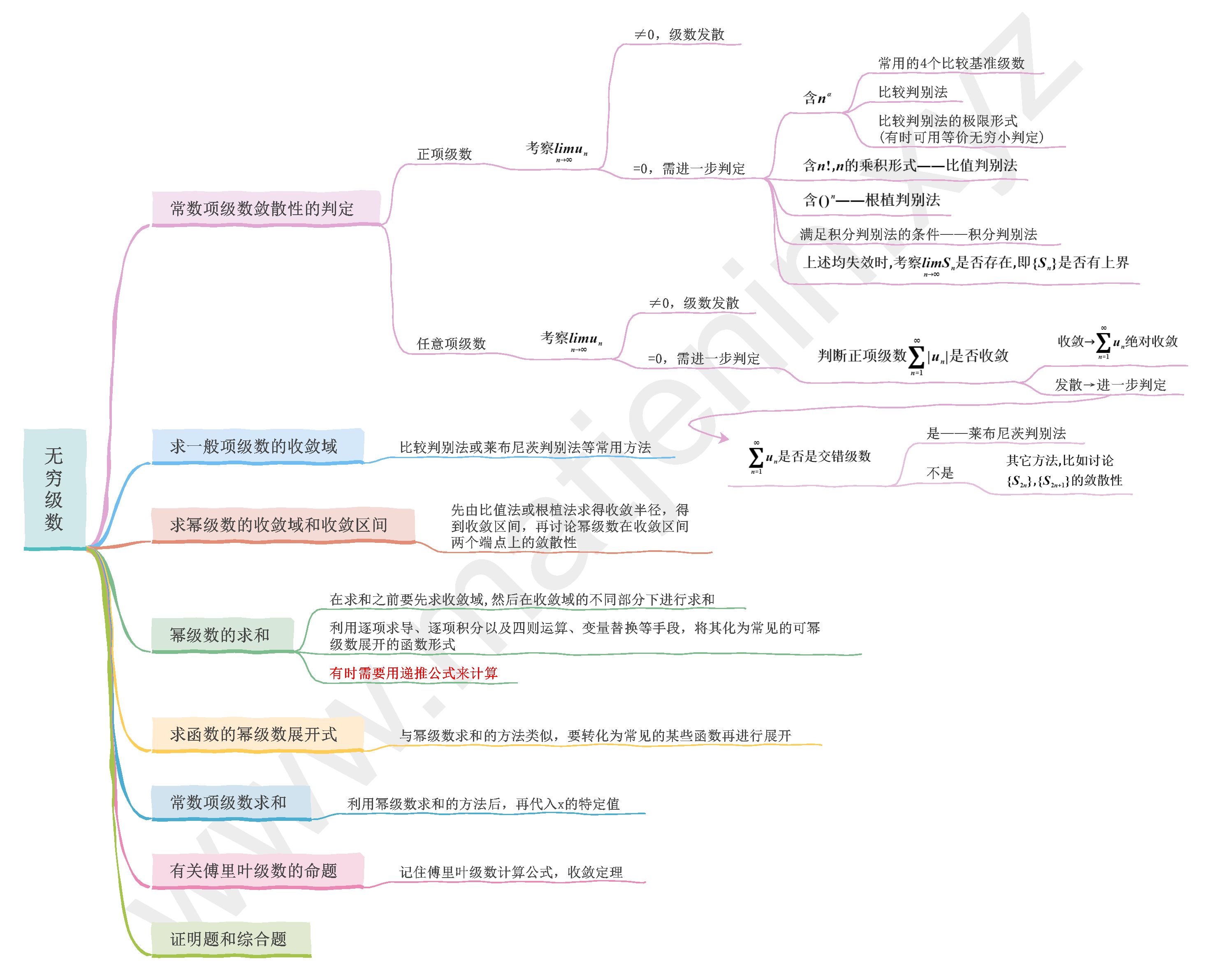
数一高数 第十章：无穷级数

第一节 常数项级数

一、级数的概念与性质

1. 级数的概念

$$\sum_{n=1}^{\infty}u_n=u_1+u_2+...+u_n+...$$

$s_n=\sum_{i=1}^nu_i$称为级数的部分和。部分和有极限，则级数收敛；反之发散。

重点在于敛散性的判定。

2. 级数的性质

• 乘以常系数、两个级数相加减。

收±收=收、收±发=发、发±发=不确定（两个都是正项级数时发散,其余情况不定）

• 在级数中增删、修改有限项不影响级数的敛散性

• 收敛级数加括号仍收敛且和不变

加括号之后收敛，原级数不一定收敛；

加括号之后发散，原级数一定发散。

• 级数收敛必要条件：$\sum_{n=1}^{\infty}u_n$收敛$→$$\lim_{n→\infty}u_n=0$

反例：$\sum_{n=1}^{\infty}\frac1n$发散

可以通过此条件判断某级数发散，即若$\lim _{n\to \infty}u_n\ne 0\to $$\sum_{n=1}^{\infty}u_n$发散

二、级数的审敛准则

1. 正项级数

$$\sum_{n=1}^{\infty}u_n,u_n\ge 0$$

基本定理：$\sum_{n=1}^{\infty}u_n$收敛$\leftrightarrow$$\{s_n\}$有上界

①. 比较判别法：大收敛推出小收敛，小发散推出大发散。

②. 比较法极限形式：设$\lim_{n→\infty}\frac{u_n}{v_n}=l(0\le l\le +\infty)$

• 若$0\lt l\lt +\infty$，则同敛散；
• 若$l=0$，则分母收敛→分子收敛，分子发散→分母发散；
• 若$l=+\infty$，则分母发散→分子发散，分子收敛→分母收敛。

有时用到的等价无穷小即属于比较法极限形式

常用的作为比较基准的级数：

1. $\sum_{n=1}^{\infty}\frac1{n^p}$，$p>1$时收敛，$p\le 1$时发散
2. $\sum_{n=1}^{\infty}aq^n(a>0,q>0)$，$q<1$时收敛，$q>1$时发散
3. $\lim_{n\to+\infty}\frac{\ln^\beta n}{n^\lambda}=\begin{cases}0&,{(\lambda>0)}\\{+\infty}&,{(\lambda<0)}&\end{cases}$
4. $\sum_{n=2}^\infty \frac1{n^p\ln^qn}\begin{cases}p>1,或p=1且q>1时收敛\\p<1,或p=1且q\le1时发散 \end{cases}$

③. 比值法：设$\lim_{n→\infty}\frac{u_{n+1}}{u_n}=ρ$，则

$$\sum_{n=1}^{\infty}u_n=\begin{cases} 收敛，&ρ<1\\ 发散，&ρ>1\\ 不一定，&ρ=1 \end{cases}$$

④. 根植法：设$\lim_{n→\infty}\sqrt[n]{u_n}=ρ$，则

$$\sum_{n=1}^{\infty}u_n=\begin{cases} 收敛，&ρ<1\\ 发散，&ρ>1\\ 不一定，&ρ=1 \end{cases}$$

如果级数中出现$a^n,n!,n^n$，则优先采用方法③④

⑤. 积分判别法：若$\exists$单调下降的正值函数$f(x)(x\ge 1)$使得$u_n=f(n)(n=1,2,3…)$，级数$\sum_{n=1}^\infty u_n=\sum_{n=1}^\infty f(n)$收敛$\Leftrightarrow \int_{1}^\infty f(x)dx$收敛

2. 交错级数

$$\sum_{n=1}^{\infty}(-1)^{n-1}u_n,u_n>0$$

莱布尼茨准则：若①.$\{u_n\}$单调减；②. $\lim_{n→\infty}u_n=0$，则$\sum_{n=1}^{\infty}(-1)^{n-1}u_n$收敛。

充分非必要，反例：$\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{2^{n+(-1)^n}}$收敛但不递减。

3. 任意项级数

概念：

绝对收敛：$\sum_{n=1}^{\infty}|u_n|$收敛，$\sum_{n=1}^{\infty}u_n$必收敛；

条件收敛：$\sum_{n=1}^{\infty}u_n$收敛，但$\sum_{n=1}^{\infty}|u_n|$发散。

基本结论：

①. 绝对收敛的级数一定收敛；

②. 条件收敛的级数的所有正项（或负项）构成的级数一定发散，即：

$$\sum_{n=1}^{\infty}u_n条件收敛→\sum_{n=1}^{\infty}\frac{u_n+|u_n|}{2}和\sum_{n=1}^{\infty}\frac{u_n-|u_n|}{2}发散$$

三、级数常用结论（强化）

2021/10/08更

①. 若$\sum_{n=1}^\infty u_n$收敛，则$\sum_{n=1}^\infty|u_n|$不定，$\sum_{n=1}^\infty (-1)^nu_n$不定（反例：$\sum_{n=1}^\infty(-1)^n/n$收敛，但$\sum_{n=1}^\infty 1/n$发散）

②. 若$\sum_{n=1}^\infty u_n$收敛，则$\sum_{n=1}^\infty (-1)^n\frac{u_n}{n}$不定（反例：$\sum_{n=2}^\infty (-1)^n\frac1{\ln n}$收敛，但$\sum_{n=2}^\infty \frac1{n\ln n}$发散）

③. 若$\sum_{n=1}^\infty u_n^2$收敛，则$\sum_{n=1}^\infty \frac{u_n}{n}$绝对收敛（$|\frac{u_n}{n}|\le \frac12(u_n^2+\frac1{n^2})$）

④. 若$\sum_{n=1}^\infty u_n$收敛，则：

$$\begin{cases} u_n\ge 0,\sum_{n=1}^\infty u_n^2收敛(\lim_{n\to\infty}u_n=0,从某项起,u_n<1,u_n^2<u_n)\\ u_n任意时,\sum_{n=1}^\infty u_n^2不定(反例: \sum_{n=1}^\infty(-1)^n\frac1{\sqrt n}收敛,但\sum_{n=1}^\infty \frac1n 发散) \end{cases}$$

⑤. 设$\sum_{n=1}^\infty u_n$收敛，则：

$$\begin{cases} u_n\ge 0时,\sum_{n=1}^\infty u_nu_{n+1}收敛(u_n\cdot u_{n+1}\le \frac{u_n^2+u_{n+1}^2}{2})\\ u_n任意时,\sum_{n=1}^\infty u_nu_{n+1}不定(反例:u_n=(-1)^n\frac1{\sqrt n}) \end{cases}$$

⑥. 设$\sum_{n=1}^\infty u_n$收敛，则：

$$\begin{cases} u_n\ge 0时, \sum_{n=1}^\infty u_{2n}, \sum_{n=1}^\infty u_{2n-1}均收敛\\ u_n任意时, \sum_{n=1}^\infty u_{2n}, \sum_{n=1}^\infty u_{2n-1}不定 \end{cases}$$

⑦. 设$ \sum_{n=1}^\infty u_{n}$收敛，则：

$$\begin{cases} \sum_{n=1}^\infty (u_{2n-1}+u_{2n}) 收敛;\\反过来若\sum_{n=1}^\infty (u_{2n-1}+u_{2n}),加上条件\lim_{n\to\infty}u_n=0,可得 \sum_{n=1}^\infty u_{n}收敛。\\ \sum_{n=1}^\infty (u_{2n-1}-u_{2n})不定; \end{cases}$$

⑧. 设$ \sum_{n=1}^\infty u_{n}$收敛，则：

$$\begin{cases} \sum_{n=1}^\infty (u_{n}+u_{n+1})收敛,\sum_{n=1}^\infty u_{n}+\sum_{n=1}^\infty u_{n+1}收敛\\ \sum_{n=1}^\infty (u_{n}-u_{n+1})收敛,\sum_{n=1}^\infty u_{n}-\sum_{n=1}^\infty u_{n+1}收敛\\ \end{cases}$$

⑨. 设$a,b,c$为非零常数，且$au_n+bv_n+cw_n=0$，则在$\sum_{n=1}^\infty u_n,\sum_{n=1}^\infty v_n$和$\sum_{n=1}^\infty w_n$中只要有两个级数收敛，另一个必收敛。

⑩. 若$\sum_{n=1}^\infty u_n$收敛，$\sum_{n=1}^\infty v_n$收敛，则

$$\begin{cases} u_n\ge 0,v_n\ge 0时,\sum_{n=1}^\infty u_nv_n收敛(u_nv_n\le\frac{u_n^2+v_n^2}{2})\\ u_n任意,v_n\ge 0,\sum_{n=1}^\infty |u_n|\cdot v_n收敛(\lim_{n\to\infty}\frac{|u_n|\cdot v_n}{v_n}=\lim_{n\to\infty}|u_n|=0)\\ u_n任意,v_n任意,\sum_{n=1}^\infty u_nv_n不定 \end{cases}$$

第二节 幂级数

一、收敛半径、区间及收敛域

幂级数定义：

$$\sum_{n=0}^{\infty}a_nx^n=a_0+a_1x+a_2x^2+...+a_nx^n+...$$

或者

$$\sum_{n=0}^{\infty}a_n(x-x_0)^n=a_0+a_1(x-x_0)+a_2(x-x_0)^2+...+a_n(x-x_0)^n+...$$

阿贝尔定理：

①. 若$\sum_{n=0}^{\infty}a_nx^n$在$x=x_0(x_0\ne 0)$处收敛，则当$|x|<|x_0|$时，$\sum_{n=0}^{\infty}a_nx^n$绝对收敛；

②. 若$\sum_{n=0}^{\infty}a_nx^n$在$x=x_0$发散，则当$|x|>|x_0|$时，$\sum_{n=0}^{\infty}a_nx^n$发散。

定理：幂级数$\sum_{n=0}^{\infty}a_nx^n$的收敛性有且仅有三种可能：

①. 对任何$x∈(-\infty,+\infty)$都收敛；

②. 仅在$x=0$处收敛；

③. 存在一个正数$R$，当$|x|\lt R$时绝对收敛，当$|x|\gt R$时发散。

定义： 正数$R$称为收敛半径， 开区间$(-R,R)$称为收敛区间， 再考察$x=\pm R$，可得收敛域。

若$\sum_{n=0}^{\infty}a_nx^n$在点$x=x_0$处条件收敛，则点$x_0$必为幂级数收敛区间$(-R,R)$的一个端点。

定理：$\lim_{n→\infty}|\frac{a_{n+1}}{a_n}|=ρ$，则$R=\frac1ρ$。

定理：$\lim_{n→\infty}\sqrt[n]{|a_n|}=ρ$，则$R=\frac1ρ$。

二、幂级数的性质

1. 有理运算性质

2. 分析性质

设幂级数$\sum_{n=0}^{\infty}a_nx^n$的收敛半径为$R$，和函数为$S(x)$，则

①. 连续性：$S(x)$在收敛区间$(-R,R)$内连续；

②. 可导性：$S(x)$在收敛区间$(-R,R)$内可导，且可逐项求导；

③. 可积性：$S(x)$在收敛区间$(-R,R)$内可积，且可逐项积分。

逐项积分通常采用定积分，幂级数的积分下限一般取0即可，详情可见：关于幂级数积分下限的讨论

三、函数的幂级数展开

$$\frac1{1-x}=1+x+x^2+...+x^n+...=\sum_{n=0}^{\infty}x^n\quad x∈(-1,1)$$ $$\frac1{1+x}=1-x+x^2+...+(-1)^nx^n...=\sum_{n=0}^{\infty}(-1)^nx^n\quad x∈(-1,1)$$ $$e^x=1+x+\frac{x^2}{2!}+...+\frac{x^n}{n!}+...=\sum_{n=0}^{\infty}\frac{x^n}{n!}\quad(-\infty<x<+\infty)$$ $$sinx=x-\frac{x^3}{3!}+...+(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}+...=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}\quad (-\infty<x<+\infty)$$ $$cosx=1-\frac{x^2}{2!}+...+(-1)^n\frac{x^{2n}}{2n!}+...=\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n}}{2n!}\quad (-\infty<x<+\infty)$$ $$\ln(1+x)=x-\frac{x^2}2+...+(-1)^{n-1}\frac{x^n}n+...=\sum_{n=1}^{\infty}(-1)^{n-1}\frac{x^n}n\quad (-1\lt x\le 1)$$ $$\begin{aligned} (1+x)^{\alpha}&=1+\alpha x+\frac{\alpha(\alpha-1)}{2!}x^2+...+\frac{\alpha(\alpha-1)...(\alpha-n+1)}{n!}x^n+...\\&=\sum_{n=0}^{\infty}\frac{\alpha(\alpha-1)...(\alpha-n+1)}{n!}x^n\\ \end{aligned}\\ (-1<x<1,区间端点待定)$$

常见幂级数的变形公式（强化）：

$$\sum_{n=1}^{\infty}\frac{x^n}n=-\ln(1-x)\\ \sum_{n=0}^\infty\frac{x^{2n}}{(2n)!}=\frac{e^{x}+e^{- x}}{2}\quad \quad\quad \sum_{n=0}^\infty\frac{x^{2n+1}}{(2n+1)!}=\frac{e^{x}-e^{-x}}{2}\\\sum_{n=0}^\infty\frac{x^n}{(2n)!}=\frac{e^{\sqrt x}+e^{-\sqrt x}}{2}$$

函数展开为幂级数的两种方法：

1. 直接展开法
2. 间接展开发（常用）

第三节 傅里叶级数

一、傅里叶系数与傅里叶级数

傅里叶系数：

$$a_n=\frac1π\int_{-π}^{π}f(x)\cos nxdx\quad n=0,1,2...$$ $$b_n=\frac1π\int_{-π}^{π}f(x)\sin nxdx\quad n=1,2...$$

傅里叶级数：

$$f(x)\sim\frac{a_0}2+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)$$

二、收敛定理（狄利克雷）

设$f(x)$在$[-π,π]$上连续或只有有限个第一类间断点，且最多只有有限个极值点，则$f(x)$的傅里叶级数在$[-π,π]$上处处收敛，且收敛于：

• $S(x)=f(x)$，当$x$为$f(x)$的连续点
• $S(x)=\frac{f(x^-)+f(x^+)}{2}$，当$x$为$f(x)$的间断点
• $S(x)=\frac{f((-π)^+)+f(π^-)}{2}$，当$x=\pm π$

三、周期为2π的函数的展开

1. [-π,π]上展开

$$a_n=\frac1π\int_{-π}^{π}f(x)\cos nxdx,\quad n=0,1,2...$$ $$b_n=\frac1π\int_{-π}^{π}f(x)\sin nxdx,\quad n=1,2...$$

奇函数：

$$a_n=0,\quad n=0,1,2...$$ $$b_n=\frac2π\int_{0}^{π}f(x)\sin nxdx,\quad n=1,2...$$

偶函数：

$$a_n=\frac2π\int_{0}^πf(x)\cos nxdx,\quad n=0,1,2$$ $$b_n=0,\quad n=1,2,...$$

2. [0,π]上展为正弦或余弦

展为正弦：

$$a_n=0,\quad n=0,1,2...$$ $$b_n=\frac2π\int_{0}^{π}f(x)\sin nxdx,\quad n=1,2...$$

展为余弦：

$$a_n=\frac2π\int_{0}^πf(x)\cos nxdx,\quad n=0,1,2$$ $$b_n=0,\quad n=1,2,...$$

四、周期为2l的函数的展开

1. [-l,l]上展开

$$a_n=\frac1l\int_{-l}^lf(x)\cos \frac{nπx}ldx,\quad n=0,1,2...$$ $$b_n=\frac1l\int_{-l}^lf(x)\sin \frac{nπx}{l}dx,\quad n=1,2...$$

奇函数：

$$a_n=0,\quad n=0,1,2...$$ $$b_n=\frac2l\int_{0}^{l}f(x)\sin \frac{nπx}ldx,\quad n=1,2...$$

偶函数：

$$a_n=\frac2l\int_{0}^lf(x)\cos \frac{nπx}ldx,\quad n=0,1,2$$ $$b_n=0,\quad n=1,2,...$$

2. [0,l]上展为正弦或余弦

展为正弦：

$$a_n=0,\quad n=0,1,2...$$ $$b_n=\frac2l\int_{0}^{l}f(x)\sin \frac{nπx}ldx,\quad n=1,2...$$

展为余弦：

$$a_n=\frac2l\int_{0}^lf(x)\cos \frac{nπx}ldx,\quad n=0,1,2$$ $$b_n=0,\quad n=1,2,...$$

技巧知识点

①. 求级数的和函数时一定要先求级数的收敛域。

②. 判断级数收敛或发散时经常用到的一个不等式关系：

$$\forall \alpha,\beta>0,a>1,\quad 当 x\to\infty时， (\ln x)^\alpha\le x^\beta\le a^x$$

常见用于判断敛散性的级数

正项级数：

$$\sum_{n=1}^\infty \frac1n\quad \sum_{n=1}^\infty\frac1{n^2}\quad \sum_{n=1}^\infty\frac1{\sqrt n}\quad \sum_{n=2}^\infty \frac1{\ln n}\quad \sum_{n=2}^\infty\frac1{n\ln n}\quad \sum_{n=1}^\infty n$$

交错级数：

$$\sum_{n=1}^\infty(-1)^n\quad \sum_{n=1}^\infty\frac{(-1)^n}{n}\quad \sum_{n=1}^\infty\frac{(-1)^n}{\sqrt n}\quad \sum_{n=2}^\infty \frac{(-1)^n}{\ln n}$$

还有这些级数的延伸、组合，比如：

$$\sum_{n=1}^\infty \frac1{n+1}\quad \sum_{n=1}^\infty\frac1{n\ln (n+1)}\quad \sum_{n=1}^\infty(\frac1n+1)\quad \sum_{n=1}^\infty(\frac1n+\frac1{n^2})$$

等等。

题型总结（强化）