微波技术 第四章 微波网络

4.1 微波网络的一般分析

4.1.1 微波网络简介

微波网络：只关心端口特性，不关心内部特性（网络内部服从麦克斯韦方程）。

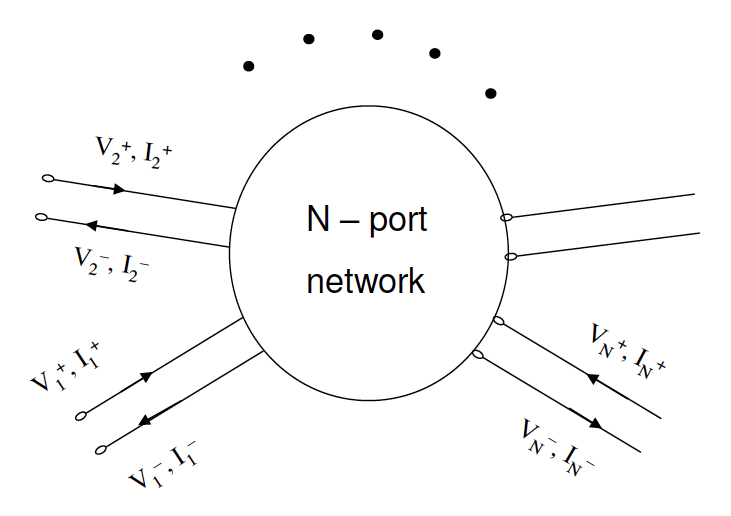
常用矩阵有Z-矩阵，Y-矩阵，S-矩阵，T-矩阵，A-矩阵。根据研究的物理量不同，引入不同的微波网络参量：

①. 研究（等效）电压、（等效）电流之间的关系： 网络的阻抗和导纳参量，对应Z矩阵和Y矩阵；

②. 研究入射波、反射波之间的关系： 网络的散射参量，对应S矩阵；

③. 研究双端口网络级联特性： 网络的转移和传输参量，对应T矩阵和A矩阵。

4.1.2 等效电压和等效电流

微波网络在各端口测量的不是场，而是（等效）电压和（等效）电流。 微波波导是广义的传输线，其基本物理量是电场和磁场。 所以需要将电压、电流与电场、磁场之间建立联系：通过功率引入等效参量。

微波波导中传输的功率为：$P=\int_S\frac12Re(E_T×H_T^\star)·\hat zdS$

传输线中传输的功率为：$P=\frac12Re(VI^\star)$

令

$$\vec E_T(x,y,z)=\vec e(x,y)V(z)\\ \vec H_T(x,y,z)=\vec h(x,y)I(z)$$

$\vec e(x,y)$和$\vec h(x,y)$是模式矢量函数，表征工作模式的场在波导横截面上的分布；

$V(z)$和$I(z)$为等效电压和等效电流，表征导行波在波导纵向上的传输特性。

代入波导传输功率表达式：

$$P=\frac12Re[V(z)I^\star(z)]\int_S(\vec e×\vec h^\star)·\hat zdS$$

归一化条件：

$$\int_S(\vec e×\vec h^\star)·\hat zdS=1$$

4.1.3 归一化等效电压和归一化等效电流

传输线上归一化电压和归一化电流仅有该处的归一化入射波a和归一化反射波b确定：

$$\overline V=\frac{V}{\sqrt{Z_0}}=\frac{V^++V^-}{\sqrt{Z_0}}=\overline V^++\overline V^-=a+b\\ \overline I=I\sqrt{Z_0}=\frac{V^+-V^-}{Z_0}\sqrt{Z_0}=\overline{V}^+-\overline V^-=a-b$$

传输线上的功率可进一步写成：

$$\begin{aligned} P&=\frac12Re(VI^\star)\\ &=\frac12Re[(\overline V^++\overline V^-)(\overline V^+-\overline V^-)^\star]\\ &=\frac12(|\overline V^+|^2-|\overline V^-|^2)\\ &=\frac12|a|^2-\frac12|b|^2 \end{aligned}$$

4.1.4 微波网络的一般形式

各端口参考面上的等效电压和等效电流分别为$V_i$和$I_i$。

$$\left[\begin{matrix} V_1\\V_2\\:\\V_N \end{matrix}\right]= \left[\begin{matrix} Z_{11}&Z_{12}&...&Z_{1N}\\ Z_{21}&Z_{22}&...&Z_{2N}\\ :&:&&:\\ Z_{N1}&Z_{N2}&...&Z_{NN}\\ \end{matrix}\right] \left[\begin{matrix} I_1\\I_2\\:\\I_n \end{matrix}\right]→ V=ZI$$

$Z_{ij}(i\ne j)$为$j$端口对$i$端口的互阻抗，$Z_{ii}$为$i$端口的自阻抗。

同理，也可用导纳矩阵$Y$来描述各参考面上电流与电压的关系：

$$I=YV$$

网络的阻抗矩阵和导纳矩阵互为逆矩阵：$ZY=I$

4.2 双端口Z矩阵和Y矩阵

4.2.1 双端口Z矩阵

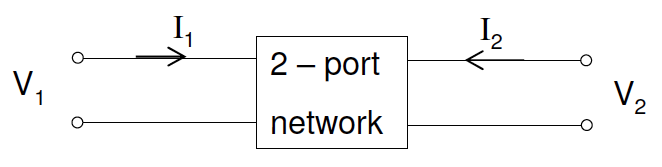
$Z$参数矩阵可表示为：

$$\left[\begin{matrix} V_1\\V_2 \end{matrix}\right]= \left[\begin{matrix} Z_{11}&Z_{12}\\ Z_{21}&Z_{22} \end{matrix}\right] \left[\begin{matrix} I_1\\I_2 \end{matrix}\right]$$ $$V_1=Z_{11}I_1+Z_{12}I_2\quad\quad V_2=Z_{21}I_1+Z_{22}I_2$$

端口2开路，$I_2=0$时，$Z_{11}\equiv \frac{V_1}{I_1}|_{I_2=0},\quad Z_{21}\equiv \frac{V_2}{I_1}|_{I_2=0}$

端口1开路，$I_1=0$时，$Z_{12}\equiv \frac{V_1}{I_2}|_{I_1=0},\quad Z_{22}\equiv \frac{V_2}{I_2}|_{I_1=0}$

4.2.2 双端口Y矩阵

$Z$参数矩阵可表示为：

$$\left[\begin{matrix} I_1\\I_2 \end{matrix}\right]= \left[\begin{matrix} Y_{11}&Y_{12}\\ Y_{21}&Y_{22} \end{matrix}\right] \left[\begin{matrix} V_1\\V_2 \end{matrix}\right]$$ $$I_1=Y_{11}V_1+Y_{12}V_2\quad\quad I_2=Y_{21}V_1+Y_{22}V_2$$

端口2短路，$V_2=0$时，$Y_{11}\equiv \frac{I_1}{V_1}|_{V_2=0},\quad Y_{21}\equiv \frac{I_2}{V_1}|_{V_2=0}$

端口1短路，$V_1=0$时，$Y_{12}\equiv \frac{I_1}{V_2}|_{V_1=0},\quad Y_{22}\equiv \frac{I_2}{V_2}|_{V_1=0}$

4.2.3 归一化阻抗参数

$$\left[\begin{matrix} \bar Z_{11}&\bar Z_{12}\\ \bar Z_{21}&\bar Z_{22} \end{matrix}\right]= \left[\begin{matrix} Z_{11}/Z_{01}&Z_{12}/\sqrt{Z_{01}Z_{02}}\\ Z_{21}/\sqrt{Z_{01}Z_{02}}&Z_{22}/Z_{02} \end{matrix}\right]$$

4.2.4 归一化导纳参数

$$\left[\begin{matrix} \bar Y_{11}&\bar Y_{12}\\ \bar Y_{21}&\bar Y_{22} \end{matrix}\right]=\left[\begin{matrix} Y_{11}/Y_{01}&Y_{12}/\sqrt{Y_{01}Y_{02}}\\ Y_{21}/\sqrt{Y_{01}Y_{02}}&Y_{22}/Y_{02} \end{matrix}\right]$$

4.2.5 归一化参数的性质

①. 互易网络：参考面所包围的区域内填充的是均匀的各项同行介质。矩阵转置是不变的。

$$Z_{ij}=Z_{ji}\quad \bar Z_{ij}=\bar Z_{ji}\quad Y_{ij}=Y_{ji}\quad \bar Y_{ij}=\bar Y_{ji}\quad(i\ne j)$$

②. 对称网络：微波网络在结构上具有面对称性或轴对称特性。对称端口互换不影响网络特性。

$$Z_{ii}=Z_{jj}\quad \bar Z_{ii}=\bar Z_{jj}\quad Z_{ij}=Z_{ji}\quad \bar Z_{ij}=\bar Z_{ji}\quad (i\ne j)\\ Y_{ii}=Y_{jj}\quad \bar Y_{ii}=\bar Y_{jj}\quad Y_{ij}=Y_{ji}\quad \bar Y_{ij}=\bar Y_{ji}\quad (i\ne j)$$

③. 无耗网络

网络的全部阻抗参量$Z_{ij},\bar{Z}_{ij}$和导纳参量$Y_{ij},\bar Y_{ij}$均为纯虚数。

4.3 S矩阵

4.3.1 S矩阵

用于分析网络端口的入射波和反射波特性。

电压波和电流波的归一化：

$$\bar V(z)=\frac{V(z)}{\sqrt{Z_0}}=\frac{V_0^+}{\sqrt{Z_0}}e^{-\beta z}+\frac{V_0^-}{\sqrt{Z_0}}e^{j\beta z}\\ \bar I(z)=\sqrt{Z_0}I(z)=\frac{V_0^+}{\sqrt{Z_0}}e^{-\beta z}-\frac{V_0^-}{\sqrt{Z_0}}e^{j\beta z}$$

归一化的入射波和反射波表示为：

$$a(z)=\frac{V_0^+}{\sqrt{Z_0}}e^{-j\beta z}\quad\quad\quad b(z)=\frac{V_0^-}{\sqrt{Z_0}}e^{j\beta z}$$ $$\bar v(z)=a(z)+b(z)\quad\quad\quad \bar I(z)=a(z)-b(z)\\ b(z)=\frac{V_0^-}{V_0^+}e^{j2\beta z}a(z)=\Gamma(z)a(z)$$

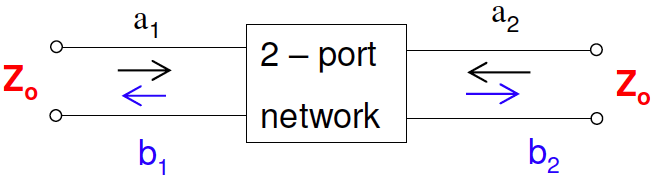
$S$矩阵可表示为$b=Sa$，即

$$\left[\begin{matrix} b_1\\b_2 \end{matrix}\right]= \left[\begin{matrix} S_{11}&S_{12}\\ S_{21}&S_{22} \end{matrix}\right] \left[\begin{matrix} a_1\\a_2 \end{matrix}\right]$$

4.3.2 S矩阵参数的物理意义

$S_{11}$：端口1的电压反射系数，$S_{11}\equiv\frac{b_1}{a_1}|_{a_2=0}$

$S_{22}$：端口2的电压反射系数，$S_{22}\equiv \frac{b_2}{a_2}|_{a_1=0}$

$S_{12}$：端口2对端口1的电压传输系数，$S_{12}\equiv \frac{b_1}{a_2}|_{a_1=0}$

$S_{21}$：端口1对端口2的电压传输系数，$S_{21}\equiv \frac{b_2}{a_1}|_{a_2=0}$

（$a_{i}\ne 0$表示端口$a_i$接微波源；$a_j=0$表示端口$a_j$不接源且负载匹配，没有入射波）

$S$矩阵不能描述级联网络。

原因：S矩阵上一级网络的输出（因变量）不能作为下一级网络的输入（自变量）。若以某一端口的入射波a和反射波b为该级网络的因变量，则该端口的入射波a和反射波b也可以作为下一级网络的自变量，从而实现对于级联网络的描述（如T矩阵）。

各端口输入输出功率：

$$P_{in,i}=\frac12a^\star_ia_i=\frac12\frac{|V^+_i|}{Z_0}\quad\quad P_{out,i}=\frac12b_i^{\star}b_i=\frac12\frac{|V_i^-|}{Z_0}$$

4.3.3 S矩阵的基本性质

（证明）

①. $S=(\bar Z-I)(\bar Z+I)^{-1}=(\bar Z+I)^{-1}(\bar Z-I)$

②. $\bar Z=(I+S)(I-S)^{-1}=(I-S)^{-1}(I+S)$

③. 若网络时互易的，S矩阵的转置就是其本身，即$S^T=S$

④. 若S矩阵满足酉条件，即$S^{\dagger}S=I$，则无耗网络$\bar Z$满足$\bar Z^\dagger=-\bar Z$（$\dagger$表示共轭转置）

⑤. 若S矩阵满足酉条件，即$S^{\dagger}S=I$，其互易性条件为：

$$\phi_{21}=\frac12(\phi_{11}+\phi_{22}\pm \pi)$$

4.3.4 阻抗匹配时的S矩阵

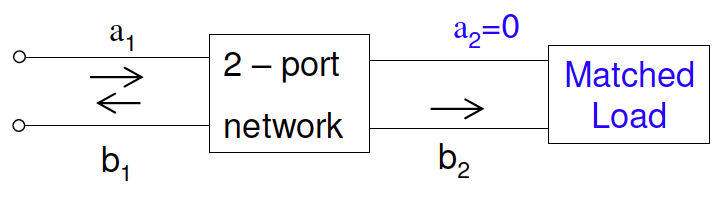
电压反射系数及回波损耗RL:

$$S_{11}\equiv \frac{b_1}{a_1}|_{a_2=0}=\Gamma\quad\quad\quad RL=10\log_{10}\frac{|a_1|^2}{|b_1|^2}|_{a_2=0}=-20\log_10|S_{11}|$$

电压传输系数及插入损耗IL:

$$S_{21}\equiv \frac{b_2}{a_1}|_{a_2=0}=T\quad\quad\quad RL=10\log_{10}\frac{|a_1|^2}{|b_2|^2}|_{a_2=0}=-20\log_10|S_{21}|$$

4.3.4 阻抗失配时的S矩阵

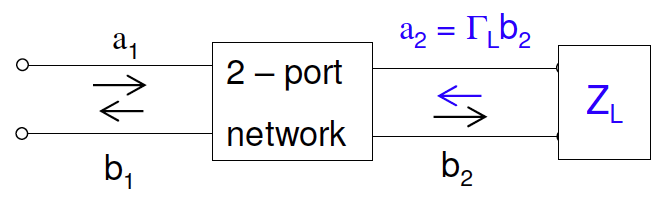
双端口电压反射系数为：

$$\Gamma_{in}\equiv \frac{b_1}{a_1}=S_{11}+\frac{S_{12}S_{21}\Gamma_L}{1-S_{22}\Gamma_L}$$

当阻抗匹配时，$a_2=\Gamma_L=0$，电压反射系数变成$\Gamma_{in}=S_{11}$

4.4 T矩阵和A矩阵

4.4.1 T矩阵

为了克服S矩阵不能描述级联网络的局限性，引入T参数矩阵：

$$\left[\begin{matrix} a_1\\b_1 \end{matrix}\right]= \left[\begin{matrix} T_{11}&T_{12}\\ T_{21}&T_{22} \end{matrix}\right] \left[\begin{matrix} b_2\\a_2 \end{matrix}\right]$$

上一级网络的反射波是下一级网络的入射波。

T参数：

$$T_{11}=\frac{a_1}{b_2}|_{a_2=0}\quad\quad\quad T_{12}=\frac{a_1}{a_2}|_{b_2=0}\\ T_{21}=\frac{b_1}{b_2}|_{a_2=0}\quad\quad\quad T_{22}=\frac{b_1}{a_2}|_{b_2=0}$$

S矩阵和T矩阵之间的相互转化（推导）：

①. 以S矩阵表示T矩阵：

$$\left[\begin{matrix} T_{11}&T_{12}\\ T_{21}&T_{22} \end{matrix}\right]=\frac1{S_{21}} \left[\begin{matrix} 1&-S_{22}\\ S_{11}&S_{21}S_{12}-S_{11}S_{22} \end{matrix}\right]$$

②. 以T矩阵表示S矩阵：

$$\left[\begin{matrix} S_{11}&S_{12}\\ S_{21}&S_{22} \end{matrix}\right]=\frac1{T_{11}} \left[\begin{matrix} T_{21}&T_{11}T_{22}-T_{12}T_{21}\\ 1&-T_{12} \end{matrix}\right]$$

4.4.2 双端口A矩阵

阻抗矩阵和导纳矩阵以电压和电流为研究对象，不足之处在于无法级联（因为自变量和因变量形式不统一，且各端口电流方向不一致），因此引入传输矩阵，即A矩阵：

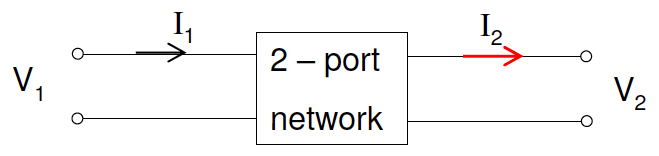
在参量矩阵互相转换时，应注意输出端口的电流方向与Z、Y、S​矩阵不同。

$$\left[\begin{matrix} V_1\\I_1 \end{matrix}\right]= \left[\begin{matrix} A_{11}&A_{12}\\ A_{21}&A_{22} \end{matrix}\right] \left[\begin{matrix} V_2\\I_2 \end{matrix}\right]$$

端口2开路，$I_2=0$：电压（传输）系数$A_{11}\equiv\frac{V_1}{V_2}$，（传输）导纳$A_{21}\equiv \frac{I_1}{V_2}|_{I_2=0}$

端口2短路，$V_2=0$：（传输）阻抗$A_{12}\equiv \frac{V_1}{I_2}|_{V_2=0}$，电流（传输）系数$A_{22}\equiv \frac{I_1}{I_2}|_{V_2=0}$

4.4.3 归一化$\bar A$矩阵

（推导）：

$$\left[\begin{matrix} \bar A_{11}&\bar A_{12}\\ \bar A_{21}&\bar A_{22} \end{matrix}\right]= \left[\begin{matrix} A_{11}\sqrt{\frac{Z_{02}}{Z_{01}}}&\frac{A_{12}}{\sqrt{Z_{01}Z_{02}}}\\ A_{21}\sqrt{Z_{01}Z_{02}}&A_{22}\sqrt{\frac{Z_{01}}{Z_{02}}} \end{matrix}\right]$$

4.4.4 $\bar A$和$\bar Z$,$\bar Y$,$S$矩阵的转换关系

在参数矩阵转换时，要注意$\bar A$矩阵的电流方向，与其它矩阵的电流方向相反。

（推导）

从$\bar Z$转换到$\bar A$：

$$\left[\begin{matrix} \bar A_{11}&\bar A_{12}\\ \bar A_{21}&\bar A_{22} \end{matrix}\right]=\frac1{\bar Z_{21}} \left[\begin{matrix} \bar Z_{11}&|\bar Z|\\ 1&Z_{22} \end{matrix}\right]$$

其中$|\bar Z|=\bar Z_{11}\bar Z_{22}-\bar Z_{12}\bar Z_{21}$

从$\bar A$转换到$\bar Z$：

$$\left[\begin{matrix} \bar Z_{11}&\bar Z_{12}\\ \bar Z_{21}&\bar Z_{22} \end{matrix}\right]=\frac 1{\bar A_{21}} \left[\begin{matrix} \bar A_{11}&|\bar A|\\ 1&\bar A_{22} \end{matrix}\right]$$

其中$|\bar A|=\bar A_{11}\bar A_{22}-\bar A_{12}\bar A_{21}$

从$\bar Y$转换到$\bar A$：

$$\left[\begin{matrix} \bar A_{11}&\bar A_{12}\\ \bar A_{21}&\bar A_{22} \end{matrix}\right]=-\frac1{\bar Y_{21}} \left[\begin{matrix} \bar Y_{22}&1\\ |\bar Y|&\bar Y_{11} \end{matrix}\right]$$

其中$|\bar Y|=\bar Y_{11}\bar Y_{22}-\bar Y_{12}\bar Y_{21}$

从$\vec A$转换到$\vec Y$：

$$\left[\begin{matrix} \bar Y_{11}&\bar Y_{12}\\ \bar Y_{21}&\bar Y_{22} \end{matrix}\right]=-\frac1{\bar A_{12}} \left[\begin{matrix} -\bar A_{22}&|\bar A|\\ 1&-\bar A_{11} \end{matrix}\right]$$

其中$|\bar A|=\bar A_{11}\bar A_{22}-\bar A_{12}\bar A_{21}$

从$S$转换到$\bar A$:

$$\left[\begin{matrix} \bar A_{11}&\bar A_{12}\\ \bar A_{21}&\bar A_{22} \end{matrix}\right]=\frac1{2S_{21}} \left[\begin{matrix} 1-|S|+S_{11}-S_{22}&1+|S|+S_{11}+S_{22}\\ 1+|S|-S_{11}-S_{22}&1-|S|-S_{11}+S_{22} \end{matrix}\right]$$

其中$|\bar S|=\bar S_{11}\bar S_{22}-\bar S_{12}\bar S_{21}$

从$\bar A$转换到$S$:

$$\left[\begin{matrix} S_{11}&S_{12}\\ S_{21}&S_{22} \end{matrix}\right]=\frac {\left[\begin{matrix} \bar A_{11}+\bar A_{12}-\bar A_{21}-\bar A_{22}&2|\bar A|\\ 2&-\bar A_{11}+\bar A_{12}-\bar A_{21}+\bar A_{22} \end{matrix}\right]} {\bar A_{11}+\bar A_{12}+\bar A_{21}+\bar A_{22}}$$

其中$|\bar A|=\bar A_{11}\bar A_{22}-\bar A_{12}\bar A_{21}$

4.4.5 A矩阵的性质

对于双端口互易网络，归一化$\bar A$矩阵的参数满足：

$$|\bar A|=\bar A_{11}\bar A_{22}-\bar A_{12}\bar A_{21}=1$$

对于双端口对称网络，归一化$\bar A$矩阵的参数满足：

$$\bar A_{11}=\bar A_{22}\quad \quad\quad |\bar A|=\bar A_{11}\bar A_{22}-\bar A_{12}\bar A_{21}=\bar A_{11}^2-\bar A_{12}\bar A_{21}=1$$

对于互易无耗网络，$\bar A_{21},\bar A_{12}$为虚数，$\bar A_{11},\bar A_{22}$为实数 （推导）。