第六章 数理统计的基本概念和抽样分布
6.1 基本概念
6.1.1 总体
总体:研究对象的某项数量指标的值的全体。
个体:总体中的每个元素。
6.1.2 样本
从一个总体$X$中随机地抽取$n$个个体$X_1,X_2,…,X_n$,由这$n$个个体组成的向量$(X_1,X_2,…,X_n)$称为总体的一个样本。样本中个体的数目称为样本容量 或 样本大小。
样本的二重性:
一方面:在一次具体的观测或试验中,得到样本的具体数据$(x_1,x_2,…,x_n)$,称为样本$(X_1,X_2,…,X_n)$的一个观测值,简称样本观测值。
另一方面:由于每个$X_i(i=1,2,…,n)$受各种随机因素的影响,因此每个$X_i$都是一个随机变量,样本$(X_1,X_2,…,X_n)$则构成一个$n$维随机变量。
(凡是离开一次具体的试验谈及样本$(X_1,X_2,…,X_n)$时,总是把样本看做随机变量)
简单随机样本:
①. 独立性:要求$(X_1,X_2,…,X_n)$是相互独立的随机变量。
②. 代表性:要求样本的每个个体$X_i$与总体$X$具有相同的分布。
(独立同分布)
6.2 统计量及分布
6.2.1 统计量
定义:设$(X_1,X_2,…,X_n)$是从总体$X$中抽取的一个样本 ,$g(x_1,x_2,…,x_n)$是实值函数且不包含任何未知参数, 则称$g(X_1,X_2,…,X_n)$为统计量。
几种常用的统计量:
第一类:样本矩
设$(X_1,X_2,…,X_n)$是从总体$X$中抽取的容量为$n$的样本:
样本均值:$\overline X=\frac 1 n \sum_{i=1}^nX_i$
样本方差:$S^2=\frac 1 {n-1}\sum_{i=1}^n(X_i-\overline X)^2$
样本标准差:$S=\sqrt{\frac 1 {n-1}\sum_{i=1}^n(X_i-\overline X)^2}$
样本的k阶原点矩:$A_k=\frac 1 n \sum_{i=1}^n X_i^k ,(k=1,2,…)$
样本的k阶中心矩:$A_k=\frac 1 n \sum_{i=1}^n (X_i-\overline X)^k ,(k=1,2,…)$
$A_1=\overline X$,$M_2=\frac {n-1}nS^2$,记$M_2$为$S_n^2$,即$S_n^2=\frac 1 n \sum_{i=1}^n(X_i-\overline X)^2$
第二类:次序统计量
定义:设$(X_1,X_2,…,X_n)$是从总体$X$中抽取的容量为$n$的样本,$(x_1,x_2,…,x_n)$是样本观测值,将样本观测值从小到大排列得到$x_{(1)}≤x_{(2)}≤…≤x_{(n)}$,令$X_{(k)}=x_{(k)},k=1,2,…,n$,则称$X_{(1)},X_{(2)},…,X_{(n)}$为样本$(X_1,X_2,…,X_n)$的次序统计量,称$X_{(i)}$为第$i$个次序统计量。
特别地,称$X_{(1)}=min\{X_1,X_2,…,X_n\}$和$X_{(n)}=max\{X_1,X_2,…,X_n\}$为最小次序统计量 和 最大次序统计量,他们的观测值分别被称为最小值和最大值。
概率密度函数:
最小次序统计量$X_{(1)}$:$f_1(x)=n[1-F(x)]^{n-1}f(x)$
最大次序统计量$X_{(2)}$:$f_n(x)=n[F(x)]^{n-1}f(x)$
6.2.2 统计中的常用分布
$χ^2$分布
定义:设随机变量$X_1,X_2,…,X_n$相互独立,且均服从$N(0,1)$分布,则随机变量
所服从的分布是自由度为$n$的$χ^2$分布,记为$Y \sim χ^2_n $。
注:$n=2$时,$χ^2_2$为$λ=\frac 1 2$的指数分布。
当$n$越来越大时,概率密度函数的曲线越来越对称。
性质:
(1). $Y \sim χ^2_n $,则$E(Y)=n$,$D(Y)=2n$。
(2). 可加性:$Y_1 \sim χ^2_m$,$Y_2 \sim χ^2_n $,且$Y_1$和$Y_2$相互独立,则$Y_1+Y_2\sim χ^2_{m+n} $
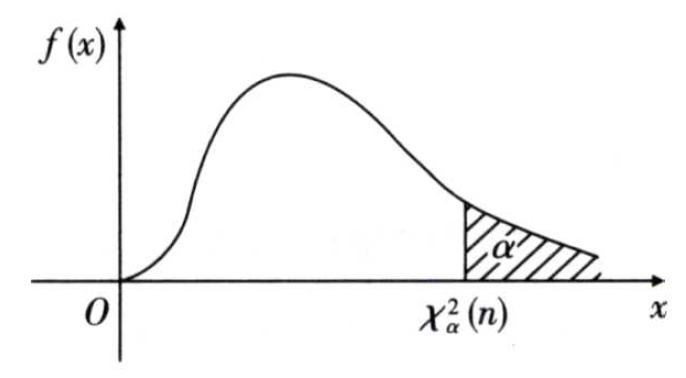
分位点:对于给定的$\alpha(0<\alpha<1)$,称满足条件
的点$χ_\alpha^2(n)$为$χ^2(n)$分布的上$\alpha$分位点。
$t$分布
定义:设随机变量$X\sim N(0,1)$,$Y \sim χ^2_n$,且$X$与$Y$相互独立,则称随机变量
所服从的分布为自由度是$n$的$t$分布,记为$T\sim t_n$。
性质:
(1). $n=1$时为柯西分布,期望方差不确定;
(2). $E(T)=0$,$D(T)=\frac n {n-2},(n>2)$;
(3). $n→\infty$时,$t$趋于标准正态分布$N(0,1)$;
(4). $t$分布的尾部比标准正态分布要厚;
(5). $t$分布的概率密度函数关于$y$轴对称。
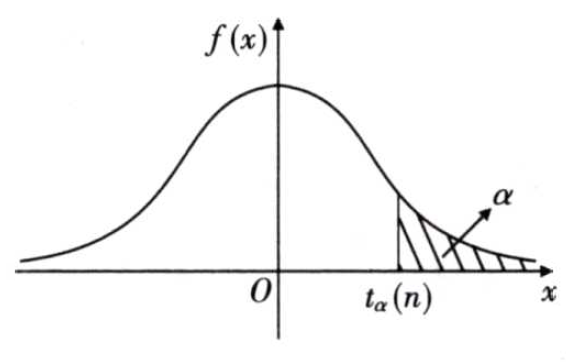
分位点:对于给定的$\alpha(0<\alpha<1)$,称满足条件
的点$t_\alpha(n)$为$t(n)$分布的上$\alpha$分位点。由$t$分布的对称性得$t_{1-\alpha}(n)=-t_{\alpha}(n)$
$F$分布
定义:设随机变量$X\sim χ^2_m$,$Y \sim χ^2_n$,且$X$与$Y$相互独立,则称随机变量
所服从的分布为第一自由度是$m$,第二自由度是$n$的$F$分布,记作$F\sim F_{m,n}$。
性质:
(1). 若$F\sim F_{m,n}(1-\alpha)$,则$1/F \sim F_{n,m}(\alpha)$;
(2). 若$T\sim t_n$,则$T^2\sim F_{1,n}$。
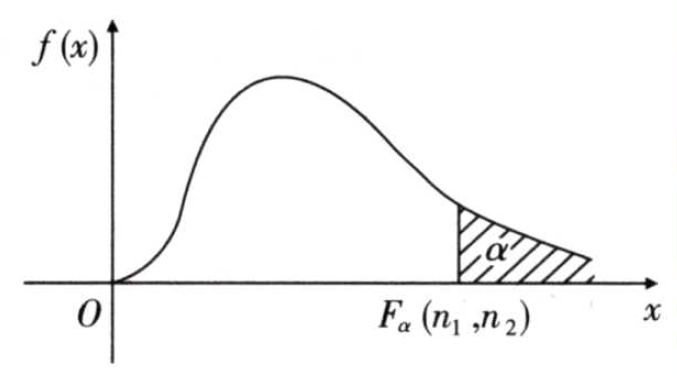
分位点:对于给定的$\alpha(0<\alpha<1)$,称满足条件
的点$F_\alpha(n_1,n_2)$为$F(n_1,n_2)$分布的上$\alpha$分位点。
6.2.3 抽样分布定理
由于统计量是随机变量,它应有确定的概率分布,成统计量的分布为抽样分布。
抽样分布定理:设$(X_1,X_2,…,X_n)$是来自正态总体$X\sim N(μ,σ^2)$的样本,样本均值为$\overline X = \frac 1 n \sum_{i=1}^nX_i$,样本方差为$S^2=\frac 1{n-1}\sum_{i=1}^n(X_i-\overline X)^2$,则
(1). $\overline X \sim N(μ,\frac {σ^2}n)$;
(2). $\frac {(n-1)S^2}{σ^2}\sim χ^2_{n-1}$,$\frac{\sum_{i=1}^n(X_i-μ)^2}{σ^2}\sim χ^2_n$;
(3). $\overline X$与$S^2$相互独立。
定理1:设$(X_1,X_2,…,X_n)$是来自正态总体$X\sim N(μ,σ^2)$的样本,样本均值为$\overline X$,样本方差$S^2$,则
定理2:$(X_1,X_2,…,X_n)$和$(Y_1,Y_2,…,Y_n)$分别是来自正态总体$X\sim N(μ,σ^2)$与$Y\sim N(μ,σ^2)$的相互独立的随机样本。令$\overline X=\frac 1 n\sum_{i=1}^n X_i$,$S_1^2=\frac 1{n-1}\sum_{i=1}^n(X_i-\overline X)^2$,$\overline Y=\frac 1 m \sum_{j=1}^{m}Y_j$,$S_2^2=\frac 1{m-1}\sum_{i=1}^m(Y_i-\overline Y)^2$,有:
(1).
(2).
(3).若$σ_1^2=σ_2^2=σ^2$,则
解题技巧
①.
②.



