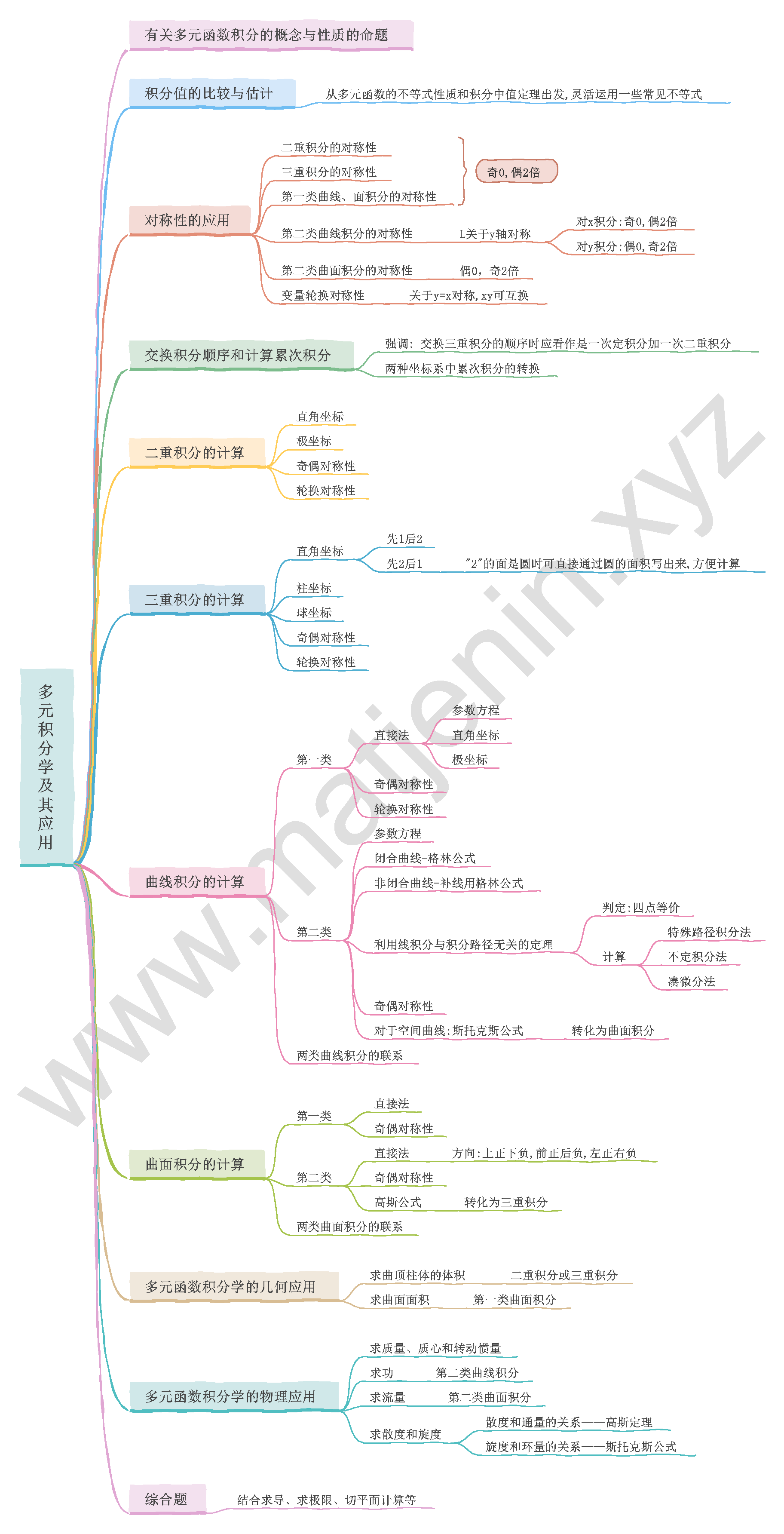
数一高数 第十二章：多元积分学及其应用

第一节 三重积分

1. 定义

$$\iiint_{Ω}f(x,y,z)dV=\lim_{λ→0}\sum_{k=1}^nf(ξ_k,η_k,ζ_k)△v_k$$

2. 性质

①. 不等式性质与二重积分类似；

②. 积分中值定理：设$f(x,y,z)$在闭区域$Ω$上连续，$V_0$为$Ω$体积，则在$Ω$上至少存在一点$(ξ,η,\gamma)$，使得

$$\iiint_Ωf(x,y,z)dv =f(\xi,\eta,\gamma)·V_0$$

3. 计算

直角坐标

①. 先一后二：

$$\iiint_{Ω}f(x,y,z)dv=\iint_{D_{xy}}dxdy\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)dz$$

②. 先二后一：

$$\iiint_{Ω}f(x,y,z)dv=\int_{c_1}^{c_2}dz\iint_{D_z}f(x,y,z)dxdy$$

有时候”先二后一”有奇效：”二”的面是圆时，可以直接通过圆的面积表示出来。

柱坐标

$$\begin{cases} x=ρ\cos \theta,&{0\le ρ< +\infty}\\ y=ρ\sin \theta,&{0\le \theta\le 2π}\\ z=z,&{-\infty<z<+\infty} \end{cases}$$

体积微元：$dv=ρdρd\theta dz$

$$\iiint_{Ω}f(x,y,z)dv=\iiint_{Ω}f(ρ\cos \theta,ρ\sin \theta,z)ρdρd\theta dz$$

适合用柱坐标的情况：

①. $\varphi (z)f(\sqrt{x^2+y^2})=\varphi(z)f(ρ)$

②. 柱体

球坐标

$$\begin{cases} x=r\sin \varphi \cos \theta,&{0\le r\lt +\infty}\\ y=r\sin \varphi\sin \theta,&{0\le \varphi\le π}\\ z=r\cos \varphi，&{0\le \theta\le2π} \end{cases}$$

体积微元：$dv=r^2\sin \varphi drd\varphi d\theta$

$$\iiint_{Ω}f(x,y,z)dv=\iiint_{Ω}f(r\sin \varphi\cos \theta,r\sin \varphi\sin \theta,r\cos\theta)r^2\sin \varphi drd\varphi d\theta$$

适合用球坐标的情况：

①. $f(\sqrt{x^2+y^2+z^2})=f(r)$

②. 球

利用奇偶性：

若积分域$Ω$关于$xOy$坐标面对称，$f(x,y,z)$关于$z$有奇偶性，则

$$\iiint_{Ω}f(x,y,z)dV=\begin{cases} 2\iiint_{D_z\ge 0}f(x,y,z)dv,&{f(x,y,z)关于z是偶函数}\\ 0,&{f(x,y,z)关于z是奇函数} \end{cases}$$

利用变量的轮换对称性

第二节 曲线积分

一、对弧长的线积分（第一类）

1. 定义

$$\int_Lf(x,y)ds=\lim_{λ→0}\sum_{i=1}^nf(\xi_i,\eta_i)△s_i$$

2. 性质

$$\int_{L(\hat{AB})}f(x,y)ds=\int_{L(\hat{BA})}f(x,y)ds（与积分路径方向无关）$$

3. 计算方法（平面）

直接法

①. 若$L:\begin{cases}x=x(t)\\y=y(t) \end{cases},\alpha\le t\le\beta$，则

$$\int_Lf(x,y)ds=\int_\alpha^\beta f(x(t),y(t))\sqrt{x'^2(t)+y'^2(t)}dt$$

原点不在圆心的圆参数方程中的参数$\theta$的几何意义是绕圆心的旋转角，和极坐标中的$\theta$不一样！（极坐标中$\theta$为绕原点的旋转角）

②. 若$L:y=y(x),a\le x\le b$，则

$$\int_Lf(x,y)ds=\int_{a}^b f(x,y(x))\sqrt{1+y'^2(x)}dx$$

③. 若$L:ρ=ρ(\theta),\alpha \le\theta \le\beta$，则

$$\int_Lf(x,y)ds=\int_\alpha^\beta f(ρ\cos \theta,ρ\sin \theta)\sqrt{ρ^2+ρ'^2}d\theta$$

利用奇偶对称性

偶2倍，奇为0

利用轮换对称性

若积分曲线关于直线$y=x$对称，则$\int_L f(x,y)ds=\int_L f(y,x)ds$

---

对空间线积分，曲线$L$的方程为：

$$\begin{cases} x=x(t)\\ y=y(t)\\ z=z(t) \end{cases} ,(\alpha\le t\le\beta)$$ $$\int_Lf(x,y,z)ds=\int_\alpha^\beta f(x(t),y(t),z(t))\sqrt{x'^2(t)+y'^2(t)+z'^2(t)}dt$$

二、对坐标的线积分（第二类）

1. 定义

$$\int_L P(x,y)dx+Q(x,y)dy=\lim_{λ→0}\sum_{i=1}^n[P(\xi_i,\eta_i)△x_i,Q(\xi_i,\eta_i)△y_i]$$

2. 性质

$$\int_{L(\hat{AB})}Pdx+Qdy=-\int_{L(\hat{BA})}Pdx+Qdy（与积分路径方向有关）$$

3. 计算方法（平面）

直接法

曲线$L:\begin{cases}x=x(t)\\y=y(t)\end{cases},t∈[\alpha,\beta]$，起点和终点对应$t=\alpha$和$t=\beta$，$P(x,y)$和$Q(x,y)$在$L$上连续，则

$$\int_L Pdx+Qdy=\int_{\alpha}^\beta [P(x(t),y(t))x'(t)+Q(x(t),y(t))y'(t)]dt$$

格林公式（建立了曲线积分和二重积分的关系）

设闭区域$D$由分段曲线$L$围成，函数$P(x,y),Q(x,y)$在$D$上具有一阶连续偏导数，则有

$$\oint_L Pdx+Qdy=\iint_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})d\sigma$$

其中$L$为$D$取正向的边界曲线。

补线用格林公式

利用线积分与积分路径无关

（1）线积分与路径无关的判定

定理：设函数$P(x,y),Q(x,y)$在单连通域$D$上有一阶连续偏导，则以下四条等价：

①. 线积分$\int_L Pdx+Qdy$与路径无关；

②. $\oint_L Pdx+Qdy=0$，其中$L$为$D$中任一分段光滑闭曲线；

③. $\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x},\forall (x,y)∈D$；

④. $P(x,y)dx+Q(x,y)dy=dF(x,y)$。

（2）计算

①. 改换路径计算：

$$\int_{(x_1,y_1)}^{(x_2,y_2)}Pdx+Qdy=\int_{x_1}^{x_2}P(x,y_1)dx+\int_{y_1}^{y_2}Q(x_2,y)dy$$

或

$$\int_{(x_1,y_1)}^{(x_2,y_2)}Pdx+Qdy=\int_{y_1}^{y_2}Q(x_1,y)dy+\int_{x_1}^{x_2}P(x,y_2)dx$$

②. 利用原函数计算：

$$\int_{(x_1,y_1)}^{(x_2,y_2)}Pdx+Qdy=F(x_2,y_2)-F(x_1,y_1)$$

奇偶对称性：

设$L$为平面上分段光滑的定向曲线，$P(x,y)$，$Q(x,y)$连续：

（1）$L$关于$y$轴对称，则

$$\int_LPdx=\begin{cases} 0,&{P关于x为奇函数}\\ 2\int_{L_1}Pdx,&{P关于x为偶函数} \end{cases} \quad\quad \int_LQdy=\begin{cases} 0,&{Q关于x为偶函数}\\ 2\int_{L_1}Qdy,&{P关于x为奇函数} \end{cases}$$

其中$L_1$是$L$在右半平面的部分。

（2）$L$关于$x$轴对称，则

$$\int_LPdx=\begin{cases} 0,&{P关于x为偶函数}\\ 2\int_{L_1}Pdx,&{P关于x为奇函数} \end{cases} \quad\quad \int_LQdy=\begin{cases} 0,&{Q关于x为奇函数}\\ 2\int_{L_1}Qdy,&{P关于x为偶函数} \end{cases}$$

其中$L_1$是$L$在上半平面的部分。

4. 计算方法（空间）

直接法

$$\begin{aligned} &\int_L P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz \\&=\int_\alpha^{\beta}\{P[x(t),y(t),z(t)]x'(t)+Q[x(t),y(t),z(t)]y'(t)+R[x(t),y(t),z(t)]z'(t)\}dt \end{aligned}$$

斯托克斯公式（建立了曲线积分和曲面积分的关系）

$L$为空间分段光滑的有向闭曲线，$Σ$为以$L$为边界的分片光滑曲面。两者方向符合右手法则。

$$\begin{aligned} &\oint_LP(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz \\&=\iint_{Σ} \begin{vmatrix} \cos\alpha&\cos\beta&\cos Υ\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\ P&Q&R \end{vmatrix} dS=\iint_{Σ} \begin{vmatrix} dydz&dzdx&dxdy\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\ P&Q&R \end{vmatrix} dS\\ &=\iint_{Σ}(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})dydz+(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x})dzdx+(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy\\ &=\iint_{Σ}\Big[(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})\cos\alpha+(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x})\cos\beta+(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})\cos \gamma\Big]dS \end{aligned}$$

5. 两类线积分的联系

$$\oint_{L{\mathop{\frown}\limits_{AB}}}Pdx+Qdy=\oint_{L{\mathop{\frown}\limits_{AB}}}(P\cos \alpha+Q\cos \beta)ds$$

其中$\cos\alpha,\cos \beta$是曲线弧${L_{\mathop{\frown}\limits_{AB}}}$沿从$A$到$B$方向的切线的方向余弦。

第三节 曲面积分

一、对面积的面积分（第一类）

1. 定义

$$\iint_{Σ}f(x,y,z)dS=\lim_{λ→0}\sum_{i=1}^nf(ξ_i,η_i,ζ_i)△S_i$$

2. 性质

$$\iint_{Σ}f(x,y,z)dS=\iint_{-Σ}f(x,y,z)dS（与积分曲面方向无关）$$

3. 计算方法

（1）直接法：$\sum:z=z(x,y),(x,y)∈D_{xy}$

$$\iint_{\sum}f(x,y,z)dS=\iint_{D_{xy}}f[x,y,z(x,y)]\sqrt{1+z_x'^2+z_y'^2}dxdy$$

（2）利用奇偶对称性：若曲面$\sum$关于$xoy$面对称，则

$$\iint_{\sum}f(x,y,z)dS=\begin{cases} 2\iint_{\sum_{z\ge 0}}f(x,y,z)dS,&{当f(x,y,z)关于z为偶函数}\\ 0,&{当f(x,y,z)关于z为奇函数} \end{cases}$$

二、对坐标的面积分（第二类）

1. 定义

$$I=\iint_{\sum}P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy$$ $$\iint_{\sum}R(x,y,z)dxdy=\lim_{λ→0}\sum_{i=1}^nR(\xi_i,\eta_i,ζ_i)(△S_i)_{xy}$$

2. 性质

$$\iint_{\sum}Pdydz+Qdzdx+Rdxdy=-\iint_{-\sum}Pdydz+Qdzdx+Rdxdy\\ （与积分曲面方向有关）$$

3. 计算方法

直接法：

（1）曲面$\sum:z=z(x,y),(x,y)∈D_{xy}$

$$\iint_{\sum}R(x,y,z)dxdy=\pm\iint_{D_{xy}}R(x,y,z(x,y))d\sigma\quad 上正下负$$

（2）曲面$\sum:x=x(y,z),(y,z)∈D_{yz}$

$$\iint_{\sum}P(x,y,z)dydz=\pm \iint_{D_{yz}}P[x(y,z),y,z]dydz\quad 前正后负$$

（3）曲面$\sum:y=y(z,x),(z,x)∈D_{zx}$

$$\iint_{\sum}Q(x,y,z)dzdx=\pm \iint_{D_{zx}}Q[x,y(z,x),z]dzdx\quad 右正左负$$

$$dydz=(-\frac{\partial z}{\partial x})dxdy\quad\quad\quad dxdz=(-\frac{\partial z}{\partial y})dxdy$$

由上式可以改变投影方向。

高斯公式（建立了曲面积分和三重积分的关系）

$\sum$为分片光滑闭曲面：（经常需要补面使用高斯公式）（其中$Ω$的正侧为外侧）

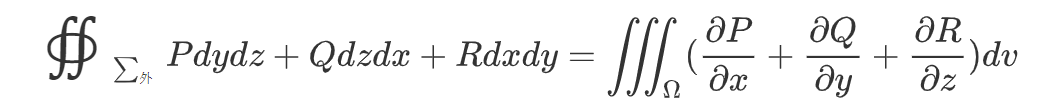
第二类曲面积分对称性的判断依据：1. 函数奇偶性；2. 积分区域法向量的方向（如果是往$D_{yz}$投影，则看曲面的法向量方向与$x$轴夹角，如果为锐角，则为正，反之为负）。

奇偶对称性：

设分块光滑定向曲面$S$关于$xy$平面对称，$S$在$xy$平面上方部分记为$S_1$（方程为$z=z(z,y),(x,y)∈D_{xy}$），下方部分记为$S_2$，又设$R(x,y,z)$在$S$连续，则有：

$$\iint_SR(x,y,z)dxdy=\begin{cases} 0,&{R关于z为偶函数}\\ 2\iint_{S_1}R(x,y,z)dxdy,&{R关于z为奇函数} \end{cases}$$

4. 两类面积分的联系

$$\iint_{\sum}(P\cos\alpha+Q\cos \beta+R\cos γ)dS=\iint_{\sum}(Pdydz+Qdzdx+Rdxdy)$$

其中$\cos \alpha,\cos \beta,\cos\gamma$是曲面$\sum$在点$(x,y,z)$处法向量的方向余弦。

第四节 多元积分应用

	平面	空间体	曲线	曲面
质心	$\overline x=\frac{\iint_D xρ(x,y)d\sigma}{\iint_D ρ(x,y)d\sigma}$	$\overline x=\frac{\iiint_Ω xρ(x,y,z)dv}{\iiint_Ω ρ(x,y,z)dv}$	$\overline x=\frac{\int_C xρ(x,y,z)ds}{\int_C ρ(x,y,z)ds}$	$\overline x=\frac{\iint_{\sum} xρ(x,y,z)dS}{\iint_{\sum} ρ(x,y,z)dS}$
转动惯量	$I_x=\iint_Dy^2ρ(x,y)d\sigma$	$I_x=\iiint_{Ω}(y^2+z^2)ρ(x,y,z)dv$	$I_x=\int_C(y^2+z^2)ρ(x,y,z)ds$	$I_x=\iint_{\sum}(y^2+z^2)ρ(x,y,z)dS$

1. 变力做功

$$力\vec F=P\vec i+Q\vec j+R\vec k\\ W=\int_{\hat{AB}}Pdx+Qdy+Rdz$$

2. 通量

$$向量场:\vec U(x,y,z)=P\vec i+Q\vec j+R\vec k\\ 通量:Φ=\iint_{\sum}Pdydz+Qdzdx+Rdxdy$$

第五节 场论初步

1. 方向导数和梯度

方向导数

$$\frac{\partial f}{\partial l}=\lim_{t→0^+}\frac{f(x_0+t\cos \alpha,y_0+t\cos\beta)-f(x_0,y_0)}{t}$$

其中$\vec e_l=(\cos \alpha,\cos\beta)$。

定理：若函数$f(x,y)$在点$P_0(x_0,y_0)$处可微，则函数在该点沿任一方向$l$的方向导数都存在，且有：

$$\frac{\partial f}{\partial l}|_{(x_0,y_0)}=f'_x(x_0,y_0)\cos\alpha+f'_y(x_0,y_0)\cos\beta$$

梯度

$$grad \ f(x_0,y_0)=f'_x(x_0,y_0)\vec i+f'_y(x_0,y_0)\vec j$$

梯度是一个向量，其方向是函数在这点方向导数最大的方向，模等于方向导数的最大值。

2. 通量和散度

设有向量场$\vec F(x,y,z)=P(x,y,z)\vec i+Q(x,y,z)\vec j+R(x,y,z)\vec k$

通量

$\vec F$沿分块光滑定向曲面$S$的通量为：

$$\begin{aligned} \iint_S\vec F\cdot \vec ndS&=\iint_S(P\cos\alpha+Q\cos\beta+R\cos\gamma)dS\\ &=\iint_SPdydz+Qdzdx+Rdxdy\\ &=\iint_S\vec F\cdot d\vec S \end{aligned}$$

其中$\vec n$是$S$上任意点$(x,y,z)$处的单位向量$\vec n=(\cos\alpha,\cos \beta,\cos \gamma)$

散度

$$div\vec F=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}$$

通量和散度的关系

由高斯公式得：

$$\iint_S\vec F\cdot \vec n dS=\iiint_Ωdiv\vec FdV$$

3. 环量和旋度

设有向量场$\vec F(x,y,z)=P(x,y,z)\vec i+Q(x,y,z)\vec j+R(x,y,z)\vec k$

环量

$\vec F$沿分段光滑定向闭曲线$\Gamma$的环量为：

$$\begin{aligned} \oint_\Gamma\vec F\cdot\vec\tau ds &=\oint_\Gamma(P\cos\alpha+Q\cos\beta+R\cos \gamma)ds\\ &=\oint_\Gamma Pdx+Qdy+Rdz\\ &=\oint_\Gamma \vec F\cdot d\vec s \end{aligned}$$

其中$\tau=(\cos\alpha,\cos\beta,\cos\gamma)$是$\Gamma$上任意点$(x,y,z)$处的单位切向量（指向曲线方向）。

旋度

$$rot\vec A=\begin{vmatrix} \vec i&\vec j&\vec k\\ \frac{\partial }{\partial x}&\frac{\partial }{\partial y}&\frac{\partial }{\partial z}\\ P&Q&R \end{vmatrix}$$

环量和旋度的关系

由斯托克斯公式得：

$$\iint_S rot\vec F\cdot \vec ndS=\int_\Gamma \vec F\cdot \vec\tau ds$$

技巧总结

①.（见李正元复习全书P247 例9.28） 当$D:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$时：

$$J=\iint_{D}(\frac{x^2}{a^2}+\frac{y^2}{b^2})dxdy=\frac{ab}2\pi$$

---

②. 平面上分段光滑曲线$L$围城平面区域$D$，则

$$D的面积=\iint_Ddxdy=\frac12\oint_{L^+}-ydx+xdy$$

其中$L^+$取正向。

③. 空间中分块光滑闭曲面$S$围成空间区域$Ω$，则

$$Ω的体积=\iiint_Ωdv=\frac13\iint_{S^+}xdydz+ydzdx+zdxdy$$

其中$S^+$取外法向。

---

④. 线积分与路径无关相关判定：

判定$\int_LPdx+Qdy$在区域$D$不是与路径无关：

• 存在分段光滑曲线$C\subset D$，$\oint_CPdx+Qdy\ne0$
• $\exists (x,y)∈D，\frac{\partial P(x,y)}{\partial y}\ne \frac{\partial Q(x,y)}{\partial x}$

判定$\int_LPdx+Qdy$在区域$D$与路径无关：

• 求得原函数$u(x,y)$使得$du=P(x,y)dx+Q(x,y)dy,(\forall (x,y)∈D)$
• 若$D$是单连通区域，有$\frac{\partial P}{\partial y}= \frac{\partial Q}{\partial x},((x,y)∈D)$
• $D=D_0/ \{M_0\}$，$D_0$单连通，若有$\frac{\partial P}{\partial y}= \frac{\partial Q}{\partial x},((x,y)∈D)$，又存在一条分段光滑闭曲线$C_0$包围点$M_0$，$\oint_{C_0}Pdx+Qdy=0$

⑤. 积分路径无关时如何求原函数

• 不定积分法：由$\frac{\partial u}{\partial x}=P(x,y)$对$x$积分得$u=\int P(x,y)dx+C(y)$，再由$\frac{\partial u}{\partial y}=Q(x,y)$，求出$C’(y)$，继而求出$C(y)$即可
• 特殊路径积分法：首先判断积分与路径无关；然后由$u(x,y)=\int_{(x_0,y_0)}^{(x,y)}Pdx+Qdy$适当选择路径求出原函数,（$(x_0,y_0)$是$D$中的定点）。

⑥. 关于多元函数积分概念上的问题：

• 若$f(x,y)$在$D$连续, $\iint_Df(x,y)dσ=0$，则$f(x,y)\equiv 0\ ((x,y)∈D)$
• 若$f(x,y)$在$D$连续，$f(x,y)>0\ ((x,y)∈D)$，则$\iint_Df(x,y)dσ>0$

上面两个命题是正确的，但是如果去掉连续的条件，就不再正确；

• 若$f(x,y)$在$D$可积，$f(x,y)\ge 0$但不恒等于$0,\ ((x,y)∈D)$，则$\iint_Df(x,y)dσ>0$

上面的命题是错误的，如果在$D$中有某个点函数值不为$0$，其它区域都为$0$，积分值仍然为$0$，即改变有限个点的函数值不改变函数的可积性及相应的积分值。

如果区间有连续的条件，就不可能存在有限个点函数值为0的情况。因为如果连续区间内一点函数值为0，那么必存在邻域，使得在这个邻域内函数值都不为0。

题型总结（强化）